Cos'è la distribuzione binomiale? Esercizi e soluzioni

Supponiamo di voler effettuare un esperimento e trarre da esso delle conclusioni statistiche su prove indipendenti l'una dall'altra.
Ogni prova che andiamo ad effettuare, può avere esclusivamente come dominio (ovvero esito) Successo o Insuccesso.
In base al campo di studio, tale esito potrà essere indicato con qualsiasi nozione.
Esempio: 0 e 1 (indicano rispettiamente INSUCCESSO e SUCCESSO)
Esempio: TRUE o FALSE (indicano rispettivamente SUCCESSO e INSUCCESSO)
Potremmo usare tantissime altre definizione (anche personalizzate) ma il concetto e lo scopo penso sia già chiaro da quanto detto già.

Tornando al nostro esperimento, supponiamo di effettuare un certo numero n di prove.
Il compito della Distribuzione Binomiale è quello fornirci il conteggio di quante volte si verifica un determinato risultato di successo in un numero fisso di prove (nel nostro caso n).

Definiamo:
n = numero di prove indipendenti 
p = probabilità di successo di una prova ( può avere valore 0 o 1, ossia insuccesso/successo)
k = esito di successo di una prova

Che tradotto in esempio:
Vuoi sapere la probabilità di ottenere esattamente 3 successi in 5 prove sapendo che la probabilità di successo di una prova è 0.5 , "k" sarebbe uguale a 3, "n" sarebbe 5, "p" sarebbe 0.5.


La formula presentata, permette appunto di calcolare quante volte si verifica un determinato risultato di successo in un numero fisso di prove.

Per chi ancora non ha affrontato il tema "coefficiente binomiale", per il nostro scopo è utile sapere che esso è definito nel seguente modo: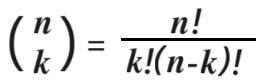


per n! fattoriale intendiamo ad esempio: 
3! = 3x2x1 = 6.

Detto ciò, facciamo un esempio di esercizio sulla distribuzione binomiale:

ESERCIZIO:
Supponiamo che la probabilità di un giocatore di fare goal calciando un calcio di rigore sia pari al 50%. Se il giocatore tenta 5 tiri totali, qual è la probabilità che ne segni esattamente 3?

DATI:
Dalla traccia del problema possiamo definire "n"=5, "p"=0.5, "k"=3

SVOLGIMENTO:
Utilizzando la formula della distribuzione binomiale per calcolare la probabilità che il giocatore segni esattamente 3 goal su 5 tentativi, basta sostituire i valori "n"=5, "p"=0.5, "k"=3 nella formula generale, ed otteremo: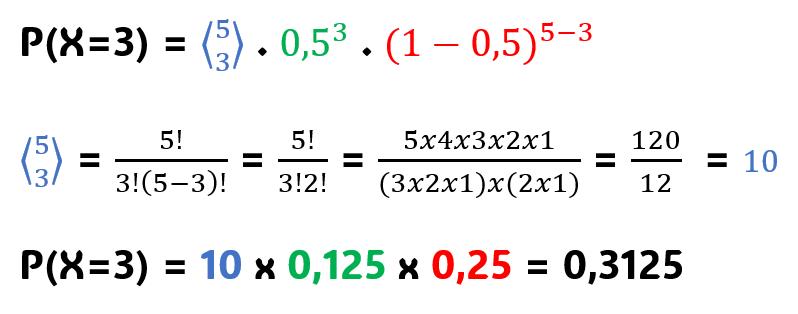

Possiamo dunque concludere che:
La probabilità che il calciatore segni 3 tiri su 5, è pari a 0,3125.