Cos'è la distribuzione binomiale? Esercizi e soluzioni (scuola secondaria)

Spiegazione per due livelli di istruzione: scuola secondaria di primo grado (con riferimento alle indicazioni nazionali DM 254 del 2012, agli obbiettivi dell'agenda 2030 dell'Unione Europea e dopo aver consultato alcuni libri di testo aggiornati) e di secondo grado (in modo diverso da come viene normalmente introdotto l'argomento).

Scuola secondaria di primo grado

La probabilità di un evento, se abbiamo un numero finito di casi, è uguale al numero di casi favorevoli diviso per il numero di casi possibili.

Ad esempio, se tiriamo in aria una moneta facendola girare, aspettiamo che cada e si fermi, e poi guardiamo la faccia in alto ci interessano due eventi: "la faccia in alto è testa", "la faccia in alto è croce". La probabilità del primo evento è 1/2=0,5 e la probabilità del secondo evento è 1/2=0,5.

Altro esempio, se tiriamo un dado e siamo interessati all'evento "sulla faccia in alto è scritto 4" allora la probabilità di questo evento è 1/6; se siamo interessati all'evento "sulla faccia in alto è scritto un numero pari" allora la probabilità dell'evento è 3/6=1/2=0,5.

La somma delle probabilità di tutti gli eventi deve essere sempre uguale ad 1, e possiamo usare questo fatto per scrivere facilmente la probabilità di eventi che sembrano difficili. Ad esempio, lanciando un dado la probabilità dell'evento "sulla faccia in alto non è scritto 2" è uguale a 1-1/6=5/6.

Cosa succede quando ripetiamo l'azione più volte?

Concentriamoci sul lancio di monete, assegniamo lettere alle quantità per essere più formali, così possiamo farci capire da qualsiasi essere umano con il nostro livello di istruzione (a questo serve la notazione matematica, per comunicare) e faticare meno nella scrittura (al posto di lunghe frasi utiliziamo poche lettere).

Abbiamo visto prima che la probabilità di ottenere testa, da ora in poi indicata con "T", con un lancio è p=0,5. La probabilità di ottenere croce, indicata con "C", è 1-p=0,5.

Se lanciamo 2 volte la moneta in momenti diversi oppure se abbiamo 2 monete e le lanciamo allora possiamo ottenere 4 sequenze di risultati: TT, TC, CT, CC. Ciascuna sequenza è quindi un evento interessante, e ciascun evento ha probabilità 1/4 di verificarsi.

Cosa succede quando lanciamo 3 monete?

Le sequenze (cioè gli eventi) possibili sono: TTT, TTC, TCT, TCC, CTT, CTC, CCT, CCC. Ci sono 8 eventi, tutti con la stessa probabilità (cioè equiprobabili), ciascuno con probabilità 1/8.

Possiamo a questo punto raggruppare le sequenze con 1, 2 o 3 lanci in un'immagine come quella qui sopra, chiamata albero binomiale. Nella figura la radice, che corrisponde a n=0, è in alto ed andando negli livelli sottostanti aumenta il numero n. Lo so, in Matematica gli alberi crescono dall'alto in basso... In ogni livello, ogni nodo ha esattamente n risultati, alcuni sono T ed altri sono C. In ciascun noto ho scritto quante teste T e quante croci C ci sono. È interessante osservare che ci sono diversi modi per raggiungere i nodi; ad esempio, per ottenere in n=3 lanci 2 teste ed 1 croce (nodo chiamato 2T 1C) posso partire da n=2 lanci da 2T e nel terzo lancio ottenere C oppure partire da 1T 1C e nel terzo lancio ottenere T. In quanti modi possiamo raggiungere un nodo? Quando sarai alla scuola secondaria di secondo grado studierai la risposta; nel mentre, se ti incuriosisce, prova a pensarci... 

A questo punto possiamo chiamare n il numero di lanci e chiederci, qual'è la probabilità che su n=3 lanci si ottengano esattamente 2 teste? Attenzione, adesso l'evento che ci interessa è più complesso di quelli visti prima perché ci sono più sequenze che rispettano le richieste dell'evento. Sempre tenendo a mente la definizione di probabilità (cioè numero casi favorevoli diviso numero casi possibili) e contando quante sono le sequenze fra quelle elencate prima che contengono 2 T otteniamo che la probabilità del nostro evento è 3/8.

Possiamo ottenere lo stesso risultato aiutandoci con la figura precedente, cioè il disegno dell'albero, basterà infatti contate i cammini (passaggi da un nodo in un livello ad uno in un livello successivo) dalla radice al nodo 2T 1C: questi sono esattamente 3.

Esercizio

Considera il lancio di 2 dadi. Sommando i numeri che ottieni ad ogni lancio, in quanti modi diversi puoi ottenere il numero 5? Qual'è quindi la probabilità di ottenere 5 in 2 lanci? Sommando i numeri dei 2 lanci, ci sono risultati che hanno probabilità maggiore di ottenere 5?

Soluzione

Scriviamo tutte le coppie di numeri che otteniamo in 2 lanci, organizzandoli per righe, e riportando il risultato dell'addizione:

1+1=2, 1+2=3, 1+3=4, 1+4=5, 1+5=6, 1+6=7,

2+1=3, 2+2=4, 2+3=5, 2+4=6, 2+5=7, 2+6=8,  

3+1=4, 3+2=5, 3+3=6, 3+4=7, 3+5=8, 3+6=9, 

4+1=5, 4+2=6, 4+3=7, 4+4=8, 4+5=9, 4+6=10,

5+1=6, 5+2=7, 5+3=8, 5+4=9, 5+5=10, 5+6=11,

6+1=7, 6+2=8, 6+3=9, 6+4=10, 6+5=11, 6+6=12.

Otteniamo quindi il risultato 5 in 4 modi diversi. Ci sono 36 casi possibili, quindi la probabilità di ottenere 5 sommando i numeri ottenuti lanciando 2 dadi è 4/36=1/9.

Osserviamo che il risultato 7 possiamo ottenerlo in 6 modi diversi, quindi ha una probabilità maggiore rispetto al risultato 5.

Esercizio (educazione finanziaria, UE Agenda 2023)

Torna nuovamente a guardare la figura dell'albero binomiale. Immagina che descriva il valore (il prezzo) di un bene nel tempo: ogni livello rappresenta un momento diverso (passare da ul livello al successivo significa far passare del tempo) e ad ogni passaggio il valore del bene può salire (questo equivale ad ottenere T) oppure scendere (ottenere C). Come il lancio di una moneta produce un risultato difficile da prevedere, così il valore di un bene è difficile da prevedere. Nell'esempio disegnato in figura, in quanti modi il valore del bene è aumentato almeno due volte?

Soluzione

Al nodo 2T 1C si arriva in 3 modi diversi, in più si può arrivare al nodo 3T in 1 solo modo. Complessivamente, ci sono 4 modi su 8 di avere almeno 2 aumenti di valore.

Scuola secondaria di secondo grado

Possiamo scrivere in modo più formale gli eventi che ci interessano definendo alcune variabili aleatorie con specifiche distribuzioni di probabilità.

La fatica nell'essere maggiormente formali sarà ripagata dall'applicare i concetti in situazioni molto diverse fra loro, di affrontare la risoluzione di esercizi più complessi e dal rendere esplicite alcune assunzioni nascoste negli esempi visti fin qui. Questo ci darà maggiore consapevolezza nell'applicare i nostri ragionamenti in contesti molto delicati (come la ricerca medica oppure la realizzazione di dispositivi di sicurezza dalla cui correttezza dipende la salute delle persone). In fin dei conti, la Matematica viene insegnata a scuola perché tutti accettano una spiegazione formale, dunque si utilizzano o producono beni e servizi con maggiore fiducia quando il loro funzionamento viene spiegato (anche) tramite una formula.

Chiamiamo X la variabile aleatoria con distribuzione di Bernoulli con probabilità di successo (cioè X=1) uguale a p, e di insuccesso (cioè X=0) uguale a 1-p. Ricordandoci che gli eventi sono insiemi, scriveremo nel seguito formalmente questo fatto con:

Nel primo esempio che abbiamo visto in questo post, cioè il lancio di una moneta, possiamo definire come successo l'ottenere T; questo avviene con probabilità p=0,5. In questo caso l'insuccesso corrisponde esattamente ad ottenere C.

Subito dopo abbiamo analizzato il lancio di un dado; se definiamo come successo l'evento "sulla faccia in alto è scritto 4" e come insuccesso "sulla faccia in alto è scritto un numero da 1 a 6 diverso da 4" allora p=1/6 e 1-p=5/6. Qui abbiamo considerato una asimmetria fra successo ed insuccesso: è molto più probabile l'insuccesso.

Naturalmente, spetta a noi definire successo/insuccesso esercizio per esercizio. Una volta fatto questo sforzo però possiamo procedere a 'velocità di crociera', visto che le proprietà di X saranno sempre le stesse.

Veniamo adesso agli eventi ripetuti, come la sequenza di lanci di moneta. Da una parte abbiamo bisogno di un modo formale per discutere molti eventi, e questo è facile perché possiamo scrivere X_1 per indicare successo/insuccesso del primo lancio, X_2 per il secondo, e così via fino a X_n per l'ultimo lancio. Dall'altra vogliamo scrivere in modo compatto la condizione che esattamente k fra gli n lanci abbiano avuto successo; come fare?

Possiamo contare il numero di successi nella sequenza sommando i valori di X_1, X_2, ..., X_n. Ogni X_i contibuisce ad un successo se X_i=1 oppure è irrilevante se X_i=0.

È importante osservazione qui che l'ordine dei lanci non ci interessa, e questo è garantito dalla proprietà commutativa dell'addizione.

Definiamo quindi la variabile aleatoria somma S come:

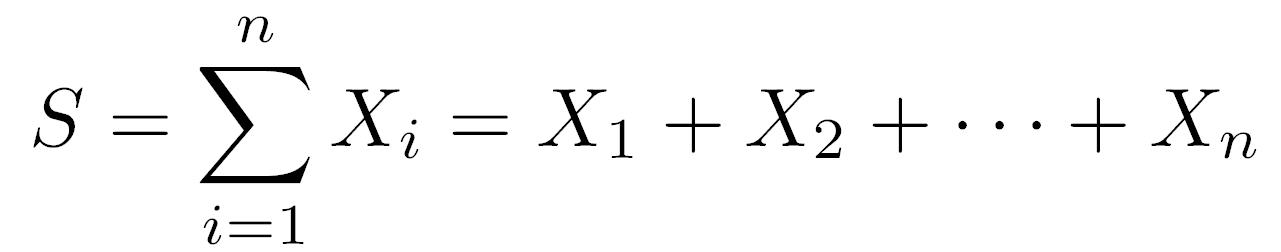
Come possiamo mettere in relazione le probabilità di successo in due lanci diversi? Se le condizioni dei lanci lo permettono, ad esempio se lanciamo la stessa moneta in momenti diversi oppure lanciamo n monete contemporaneamente in modo che non si tocchino mai, allora possiamo assumere che gli eventi di successo/insuccesso di una moneta siano indipendenti dai successi/insuccessi delle altre monente o della stessa moneta in momenti diversi.

Questa è l'assunzione nascosta nel discorso che abbiamo svolto fino a qui. Bisogna fare molta attenzione alle assunzioni da cui dipendono le formule che usiamo nelle applicazioni e negli esercizi perché sta al nostro buon senso (e spirito critico) decidere se in una determinata situazione le assunzioni sono ragionevoli. Ad esempio, se per far prima mettiamo tutte le n monete in una scatola e poi le lanciamo insieme allora il volume della scatola influenzerà il lancio. Il caso estremo è quello di una scatola cilindrica con sezione poco più grande del diametro delle monete: queste saranno in contatto per la maggior parte del lancio e dunque il successo di una avrà un grande impatto sul successo delle altre.

Come è noto, la probabilità congiunta di due eventi indipendenti è uguale al prodotto delle probabilità dei singoli eventi. Formalmente possiamo scrivere, considerando che gli indici i e j prendono valori interi da 1 a n, in formula questa frase con:

Con l'assunzione di indipendenza (questa volta esplicita) abbiamo che S è la somma di n variabili aleatorie indipendenti ed ugualmente distribuite Bernulli con probabilità di successo p. Se compiamo n lanci ed esattamente i primi k lanci mi danno successo (dunque gli ultimi n-k lanci danno insuccesso) allora:

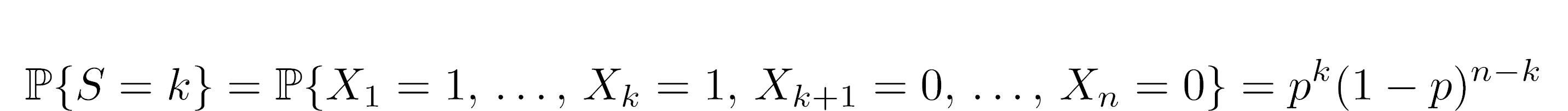
Tuttavia, ci sono molti modi in cui esattamente k lanci su n hanno successo. Quanti? È noto che ci sono

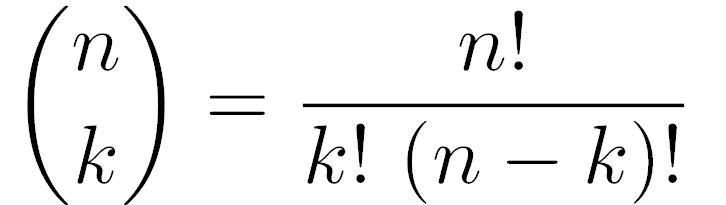
combinazioni con esattamente k successi su n lanci. Abbiamo ripassato così il coefficiente binomiale. Dunque S ha distribuzione Binomiale con

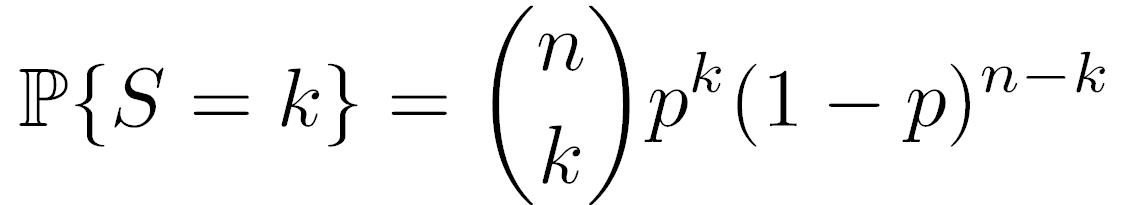
Esercizio 

Durante lo sviluppo di software che implementano funzioni di sicurezza, come ad esempio l'attivazione del freno automatico in un auto con guida assistita, ha un ruolo molto importante la seguente prova: la funzione deve essere attivata n volte di seguito e tutte le n volte non deve fallire, cioè deve funzionare come ci si aspetta. Se il prototipo non supera questo test deve essere rivisto in modo sostanziale, e questo può farne aumentare notevolmente il costo. La probabilità di insuccesso 1-p per ogni attivazione della funzione viene normalmente fissata da uno standard internazionale, ad esempio nello standard IEC 61508-7 aggiornato al 2010 leggiamo che per applicazioni con SIL 3 (come ad esempio ...) la probabilità di insuccesso deve essere minore di 0,0001. Assumendo che chiamate successive della funzione di sicurezza siano indipendenti, quante volte deve essere chiamata (sempre con successo) la funzione per avere ottenere una probabilità minore o uguale a 0,05?

Svolgimento

In questo esercizio applicare la binomiale è semplice perché il numero di successi deve essere uguale al numero di lanci k=n, e dunque

Quindi, applicando le proprietà della radice n-esima e del logaritmo, otteniamo

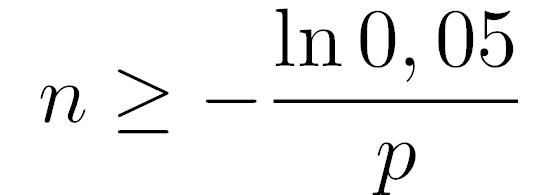
Con i numeri dell'esercizio, per star tranquilli abbiamo bisogno di circa n=10000 prove!

Esercizio

Considera lo sviluppo di una funzione critica, cioè un servizio il cui buon funzionamento (la funzione quando viene valutata restituisce il risultato corretto) garantisce la salute, la sicurezza oppure il reddito delle persone. Ad esempio un servizo bancario dove la funzione che verifica il credito dell'utente è critica, oppure un servizio sanitario dove la funzione prenota in automatico una visita sulla base del risultato delle analisi di un paziente. Per ottenere una probabilità di insuccesso quando la funzione viene valutata (cioè di fallimento del servizio) più piccola di un cero valore (valori tipici sono 0,0001 o 0,00001) possiamo seguire almeno due strade. O investiamo molti soldi nel costruire un'unica implementare della funzione che sia molto affidabile, oppure costruiamo più implementazioni della stessa funzione e confrontiamo fra loro i risultati per restituire all'utente/paziente il risultato ottenuto nella maggioranza dei casi. Quest'ultima soluzione (qui descritta in modo poco formale) si chiama N-Version Programming (NVP) ed è molto utilizzata in pratica. La domanda è: in quali condizioni conviene implementare una sola volta la funzione? In quali conviene l' NVP? Concentrati sul caso più semplice: vogliamo tollerare f=1 insuccessi fra i risultati di n=2f+1=3 implementazioni, e quindi consideriamo la maggioranza di m=2 implementazioni su n=3.

Svolgimento

Utilizziamo la definizione di probabilità della distribuzione binomiale vista prima. In particolare, possiamo scrivere la probabilità che almeno 2 su 3 dei risultati in NVP con n=3 siano corretti (che viene chiamata reliability, ed indivata con R):

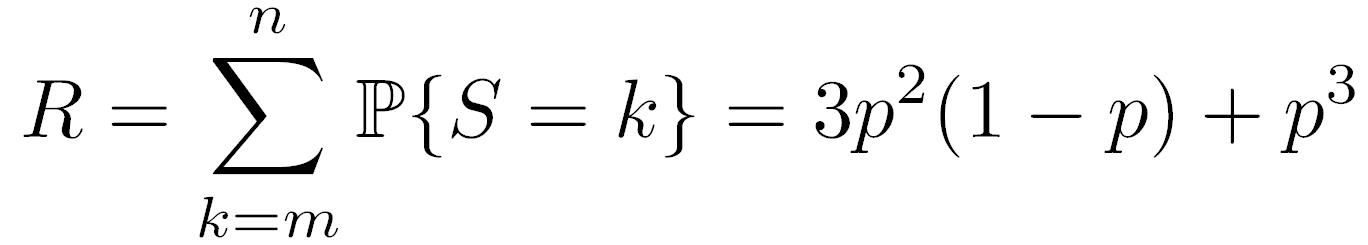Ci chiediamo quindi quando la singola implementazione è migliore di NVP con n=3, cioè quando la seguente disuguaglianza è vera:

Portando a sinistra del maggiore o uguale tutti i fattori otteniamo:

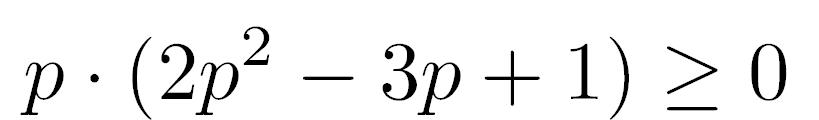
Sappiamo che la probabilità p è compresa fra 0 ed 1, ed consideriamo sia strettamente maggiore di zero (altrimenti non avrebbe senso sviluppare le implementazioni della funzione). Dunque possiamo trovare i due valori di p che delimitano la regione in cui vale la disuguaglianza: risolviamo la corrispondente equazione di secondo grado!

Otteniamo che p è uguale a 1/2=0,5 oppure 1. La probabilità non può essere maggiore di 1, dunque la regione che ci interessa, quella per cui conviene sviluppare un'unic implementazione della funzione, è 0<p<=0,5. Questo ci dice che sostanzialmente non coniene una singola implementazione, visto che la probabilità 1/2 è quella di un tiro di una moneta, e le funzioni critiche normalmente richiedono probabilità di successo molto maggiore. 

In generale, quando n>3 per tollerare f>1 insuccessi, oppure quando non possiamo assumere che i risultati siano indipendenti, l'analisi è più complicata. Spero che questo esercizio ti dia l'idea delle grandi possibilità che si aprono con lo studio della Matematica. In fin dei conti, poter contribuire allo sviluppo della società, per esempio rendendola più sicura, è uno dei migliori scopi dello studio.

Esercizio (con soluzione che dipende dall'andamento di un esperimento)

Torniamo a riflettere (anzi a sperimentare!) sull'assunzione di indipendenza fra gli eventi. Procurati due o tre scatole di volume diverso. Raccogli 5 monete tutte uguali, ad esempio 5 monete da 5 centesimi di Euro, e con un pennarello etichetta ogni moneta (ad esempio disegnando un puntino sulla prima moneta, due puntini sulla seconda, etc). Prova a lanciare 20 volte le 5 monete usando la prima scatola. Con grande pazienza, annota tutti i risultati. Puoi aiutarti con un foglio elettronico, anche se puoi usare semplicemente carta e penna. Ripeti poi la stessa procedura con la seconda scatola, ed eventualmente con la terza scatola. Aiutandoti con la seguente formula poi rispondere alla domanda: gli eventi osservati sono indipendenti? Esiste veramente una dipendenza della dipendenza (misurata rispetto a quanto i numeri a sinistra ed a destra del punto interrogativo sono diversi) rispetto al volume della scatola?

Sviluppi futuri

In un seguente post riprenderò la descizione della distribuzione binomiale a livello universitario ed aziendale.