LE EQUAZIONI DI TERZO GRADO, OVVERO COME AFFRONTARE UN BOSS DI TERZO LIVELLO

Cosa fare quando una mite e semplice equazione che tutti sappiamo risolvere evolve fino allo stadio del Super Saiyan di terzo livello? Per fortuna risolvere una equazione di terzo grado è un compito assai più semplice che affrontare uno scimmione biondo con i capelli lunghissimi e basterà tenere in mente alcune semplici regole.

Sappiamo infatti come risolvere in maniera metodica sia le equazioni di primo grado che le equazioni di secondo grado, perciò nel caso di equazioni di grado superiore, dobbiamo fissarci come obiettivo principale quello di ricondurci allo studio di qualcosa che sappiamo trattare.

In poche parole quindi risolvere una equazione di terzo grado equivarrà a riformulare l'equazione come un prodotto di una equazione di secondo grado e di una equazione di primo grado.

Raggiungere questo obiettivo non sempre è possibile nel campo dei numeri reali o senza l'ausilio di un calcolatore, perciò se dopo svariate prove vi risulta impossibile effettuare la scomposizione a mano, state tranquilli, è tutto normale!

In ogni caso, la maggior parte degli esercizi che vi troverete ad affrontare a livello scolastico accetta una soluzione che è possibile calcolare con le vostre sole forze, perciò cerchiamo di capire come fare con pochi, semplici esempi!

CASO 1 (quando siete fortunati): Equazione di terzo grado SPURIA

Se vi ritrovate con un caso simile di fronte, esultate! Siete al cospetto dell'equazione di terzo grado più semplice da risolvere.

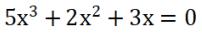
Come potete vedere nell'immagine qui sopra, un'equazione spuria è quella in cui il termine noto è nullo, perciò abbiamo solo i termini in x. Possiamo raccogliere dunque la x e ricondurci al prodotto di una equazione di primo grado e di una equazione di secondo grado.

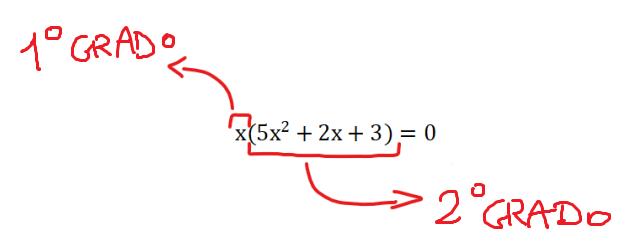
Ed ecco quindi che il problema di risolvere l'equazione di terzo grado viene ricondotto a qualcosa che sappiamo risolvere:

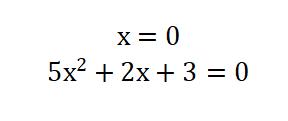
Delle tre soluzione dell'equazione di terzo grado, una è la più banale x=0 mentre le altre due ricaviamo che non sono reali (infatti l'equazione di secondo grado 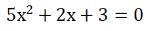 non ammette soluzioni reali poiché il suo discriminante è negativo!).

CASO 2 (quando la vostra fortuna non si è ancora esaurita): Equazione di terzo grado BINOMIA

Un altro caso molto semplice per risolvere una equazione di terzo grado in pochi passaggi è quando questa si trova nella forma binomiale.

Un’equazione del tipo

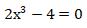
è infatti già pronta per essere risolta! Basterà isolare la 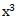 al primo membro

da cui

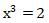
ed eseguire l’operazione di radice cubica su entrambi i membri, perciò le soluzioni saranno:

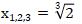
Come interpretare questi risultati? È semplice, significa che le equazioni in forma binomiale hanno sempre tre soluzioni e queste sono tutte uguali e coincidenti! 

Nella vita però non sempre siamo così fortunati, perciò nel caso in cui ci trovassimo di fronte ad un'equazione di terzo grado completa, dobbiamo individuare un metodo più generico per scomporla e risolverla.

CASO 3: EQUAZIONE DI TERZO GRADO COMPLETA E SCOMPOSIZIONE CON IL METODO DI RUFFINI

Tenendo sempre a mente l'obiettivo finale, ossia ritrovarci con un prodotto di due equazioni che sappiamo risolvere, il metodo di Ruffini si propone di fare proprio questo.

Come ci hanno insegnato a fare alle scuole elementari con i numeri, anche con i polinomi è possibile applicare l'operazione di divisione.

Se il nostro polinomio di terzo grado fa le veci del dividendo, con il metodo di Ruffini dobbiamo trovare un divisore e il relativo quoziente che diventeranno i due nuovi fattori da studiare.

Prendiamo in studio la seguente equazione di terzo grado:

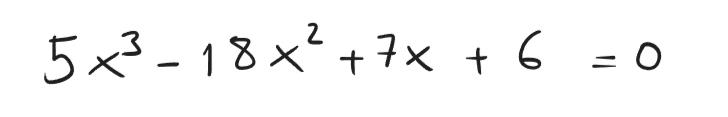
Se la nostra equazione è il dividendo, il nostro obiettivo è trovare un divisore e quindi un quoziente in modo tale che la divisione tra polinomi restituisca resto nullo.

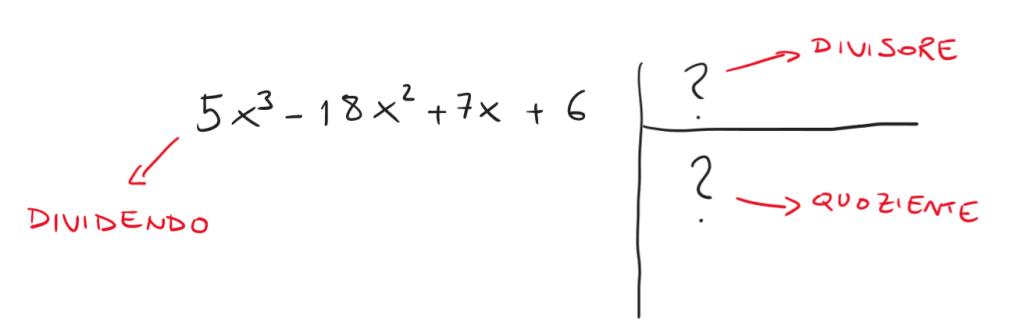
Per farlo, possiamo utilizzare il metodo di Ruffini che consiste nel creare una tabella con i coefficienti della nostra equazione disposti sulla prima riga

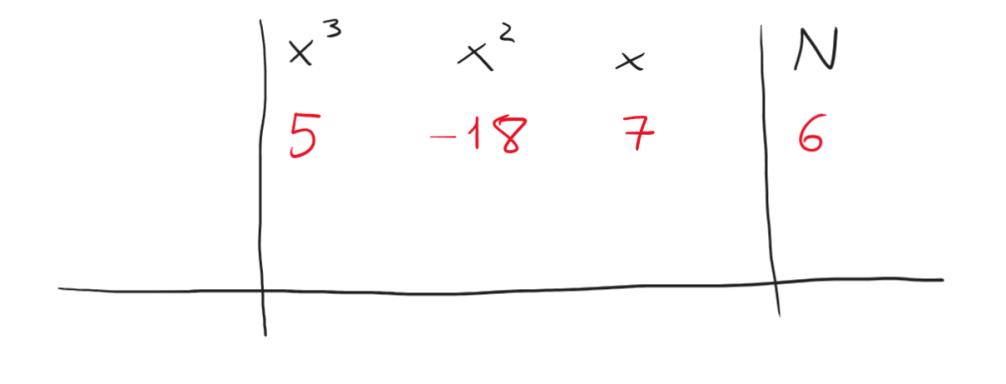
Fatto questo semplice passaggio, l’obiettivo sarà quello di riempire la seconda riga con nuovi coefficienti, calcolati a partire da un termine inserito nella prima colonna.

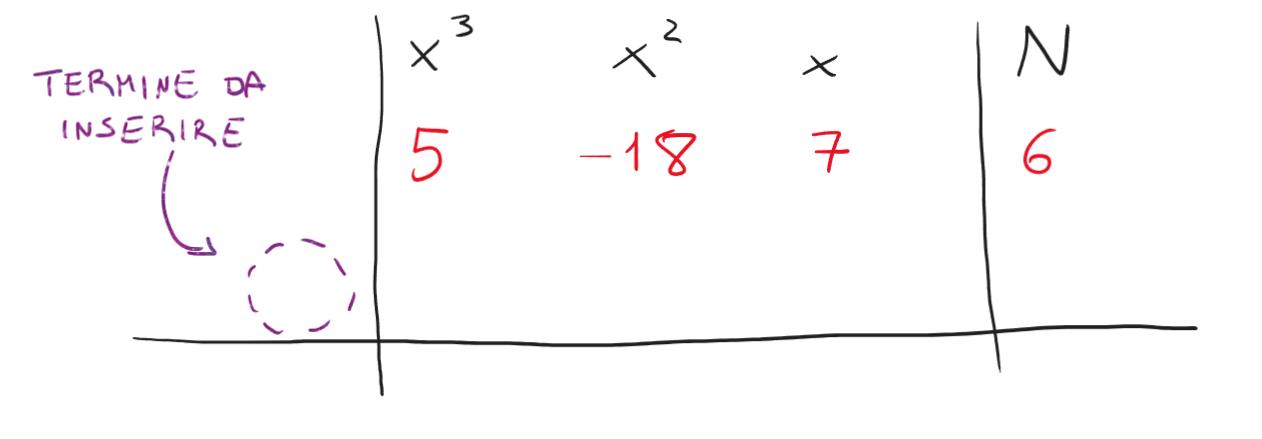
La prima cosa da fare sarà quindi scegliere il nostro termine, che chiameremo “moltiplicatore”. Come scegliere il moltiplicatore? Non c’è una vera e propria regola per farlo, bisognerà andare a tentativi, ma un trucco consiste nell’andare a guardare il termine noto N della nostra equazione. In questo caso, N è pari a 6 per cui molto probabilmente il moltiplicatore che ci consentirà di ottenere una divisione con resto nullo sarà un numero intero compreso nel range [-6,6], ossia uno tra i numeri -6, -5. -4, -3, -2, -1, 1, 2, 3, 4, 5, 6.

Come sapremo di aver scelto il numero giusto? È semplice, se alla fine di tutti i nostri calcoli avremo scritto nella seconda riga dell’ultima colonna un numero uguale al nostro termine noto, allora avremo fatto centro! In caso contrario, dovremo ricominciare da capo scegliendo un altro moltiplicatore.

Andiamo a fare un esempio e vediamo come calcolare i coefficienti da inserire nella seconda riga.

Scegliamo ad esempio un moltiplicatore pari a 2 e scriviamolo nella prima colonna: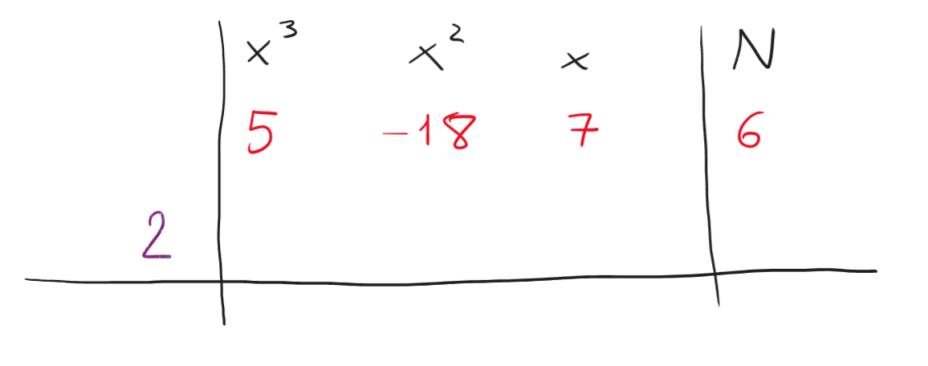

Il coefficiente di grado 3, che nel nostro caso vale 5, lo riportiamo così com’è nella terza riga.

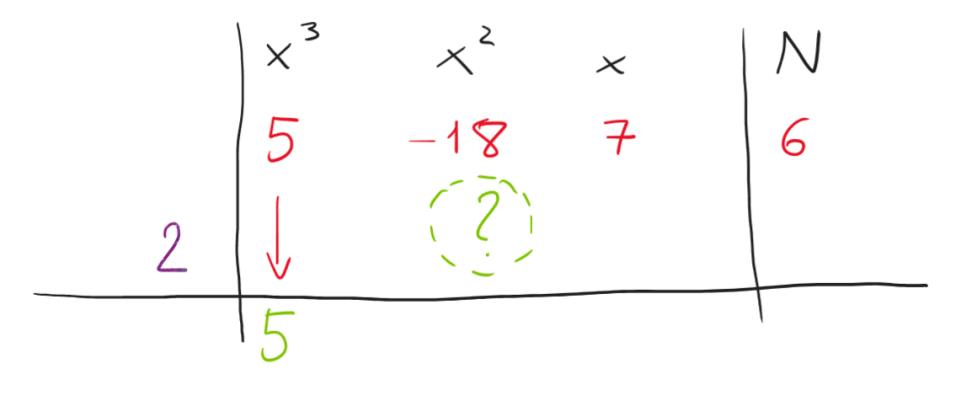
Adesso, come calcoliamo il coefficiente di grado due da inserire nella seconda riga della nostra tabella (il coefficiente andrà quindi calcolato e riportato sotto il -18, al posto del punto interrogativo verde che vedete nella figura in alto)?

È qui che interviene il “moltiplicatore” il cui nome non è stato scelto a caso! Dovremo infatti moltiplicare l’ultimo coefficiente riportato nella terza riga (nel nostro caso l’ultimo numero scritto è il 5 in verde) per il moltiplicatore stesso, ossia dovremo scrivere il risultato della semplice moltiplicazione 5*2 che fa 10.

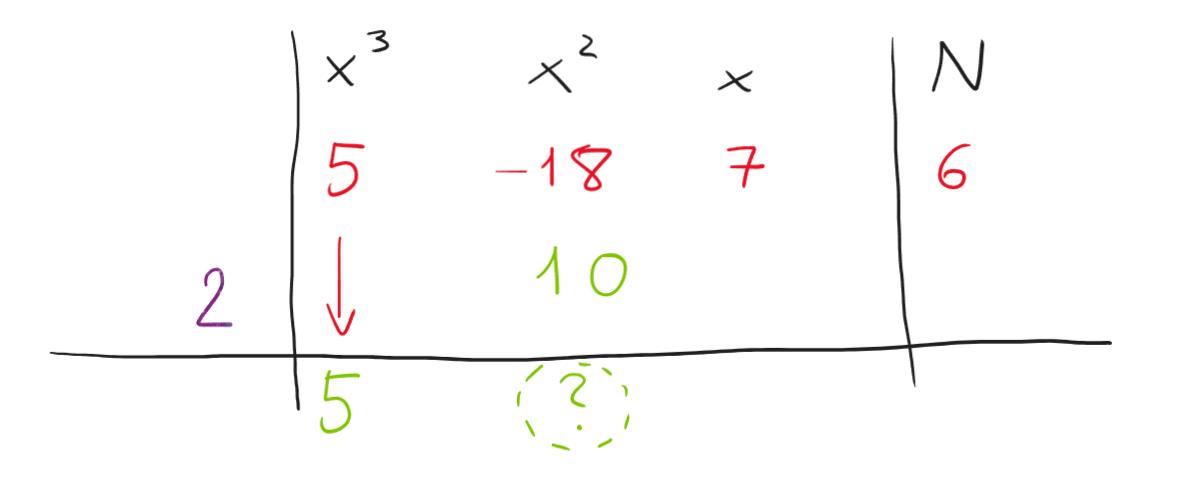
Adesso siamo pronti a calcolare il nostro nuovo coefficiente da inserire nella terza riga (punto interrogativo verde). Come? Basterà sottrarre i numeri che vediamo incolonnati sopra, ossia -18 e 10. -18-10=-28

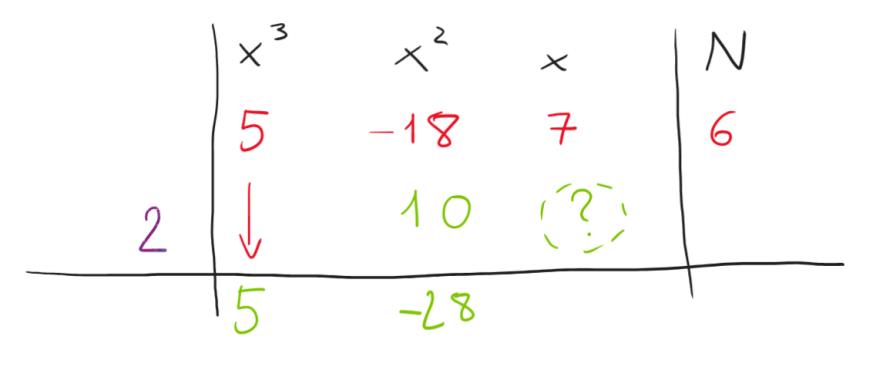
Tocca alla terza colonna adesso, ma ormai abbiamo capito il procedimento. Moltiplichiamo di nuovo l’ultimo numero calcolato e scritto nella terza riga per il nostro moltiplicatore, perciò -28*2=-56 e scriviamolo nella seconda riga, al posto del nostro punto interrogativo verde

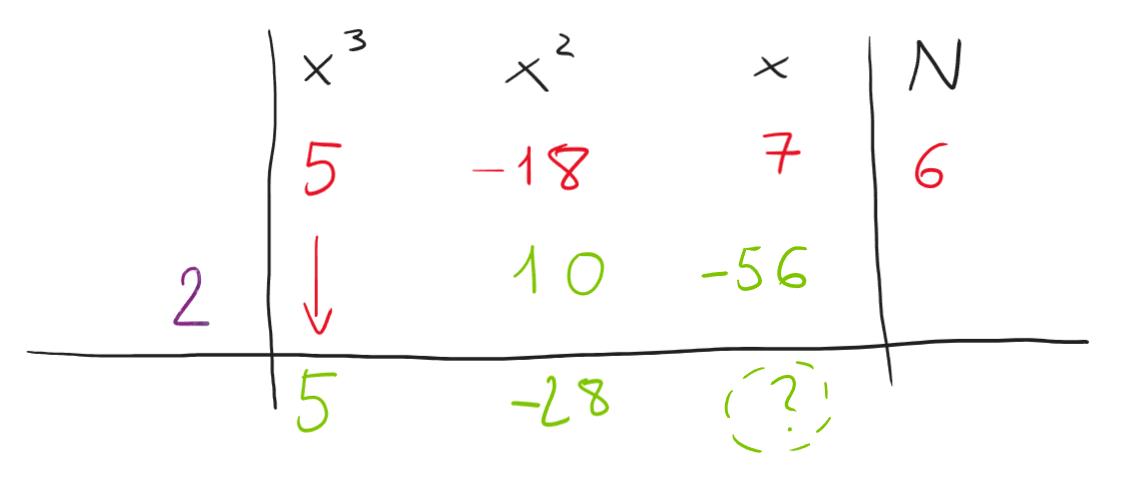
Esattamente come prima, sottraiamo i numeri incolonnati nella terza colonna e calcoliamo il nuovo coefficiente da scrivere in terza riga. Facciamo quindi l’operazione 7-(-56) ossia 7+56=63

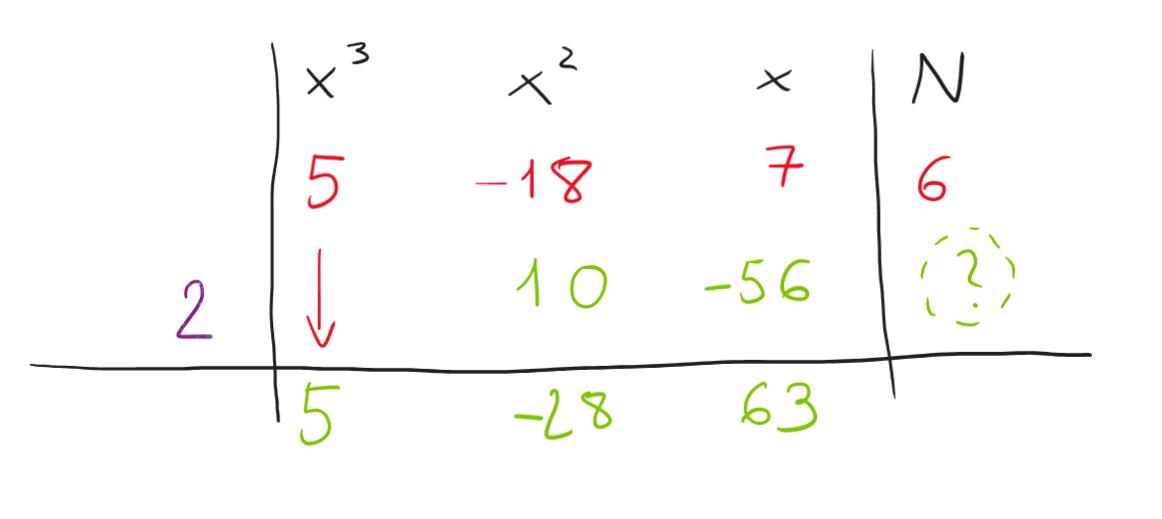
Siamo all’ultimo passaggio, occorre ora moltiplicare 63*2=126 e riportarlo nella colonna del termine noto

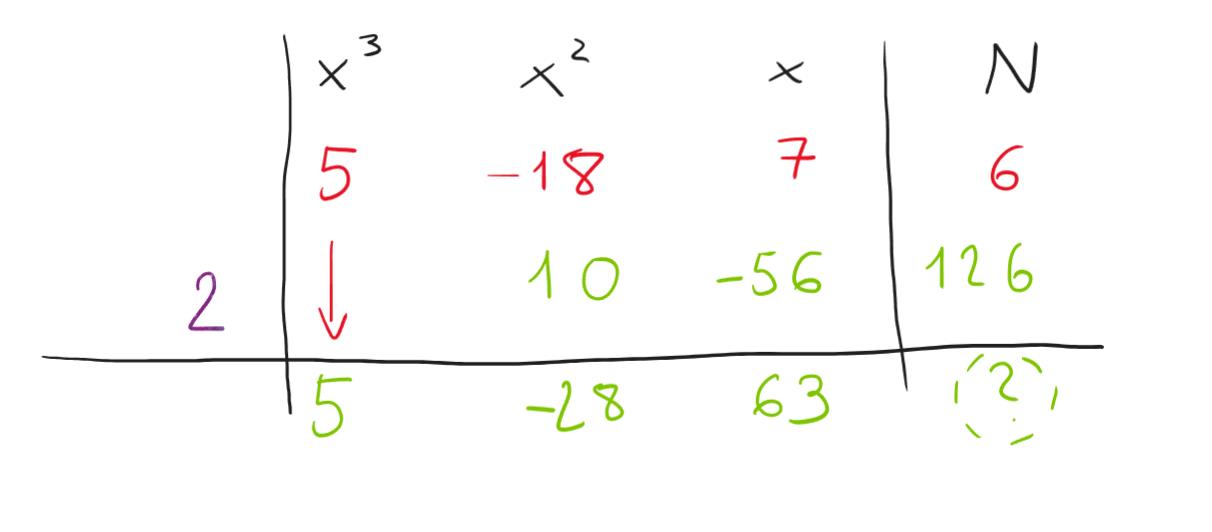
Effettuando l’ultima sottrazione 6-126=-120 ci rendiamo conto che non abbiamo ottenuto zero nell’ultima casella, perciò il moltiplicatore scelto inizialmente era sbagliato.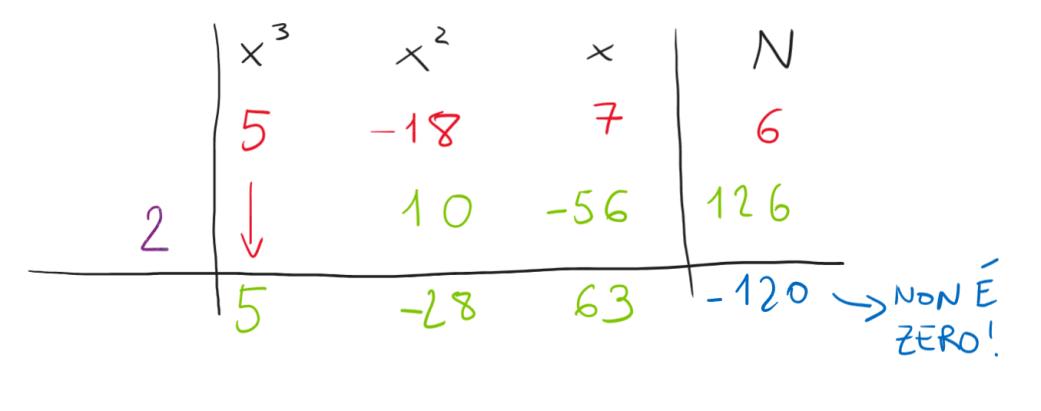

Questa è una cosa che può capitare dovendo procedere a tentativi, ma non disperiamoci, scegliamo un altro moltiplicatore e ripetiamo il procedimento appena imparato! Proviamo scegliendo come moltiplicatore il 3

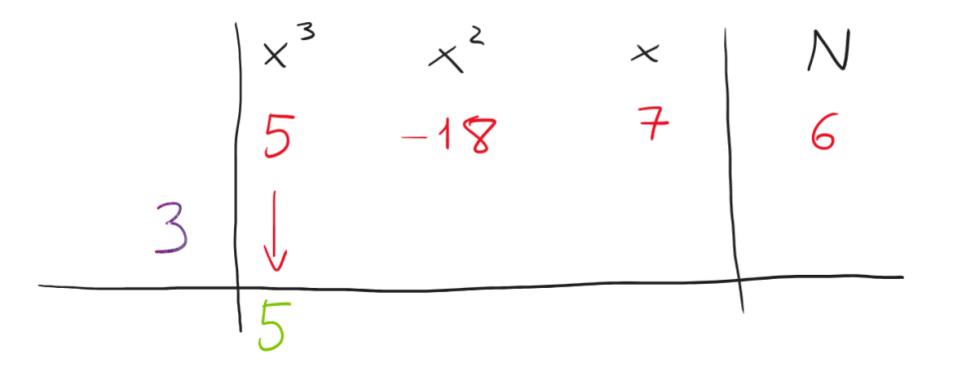
Ormai ci abbiamo preso la mano no? Sappiamo come agire! Moltiplichiamo e sottraiamo! 3*5=15 e poi ancora -18-15=-33

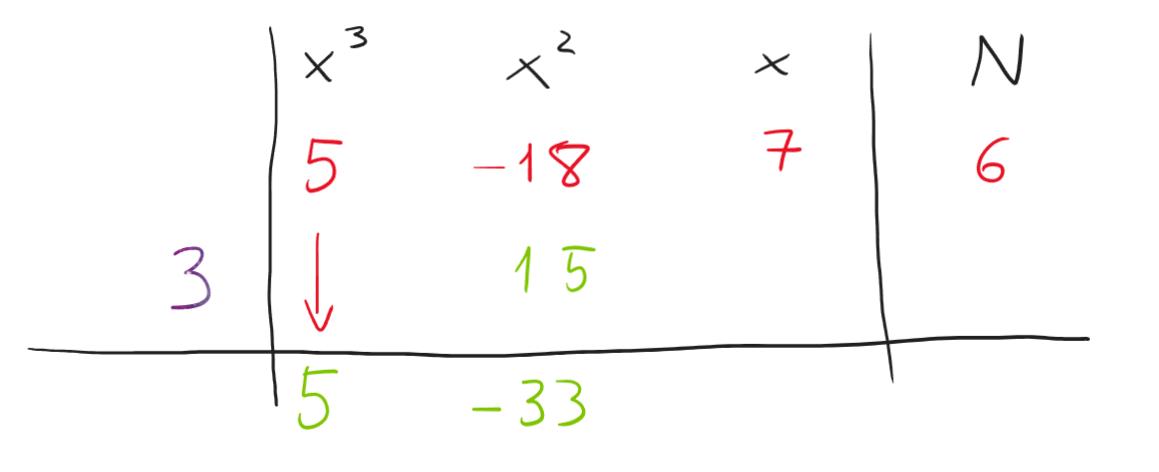
E ancora, -33*3=-99 e quindi 7-(-99)=106

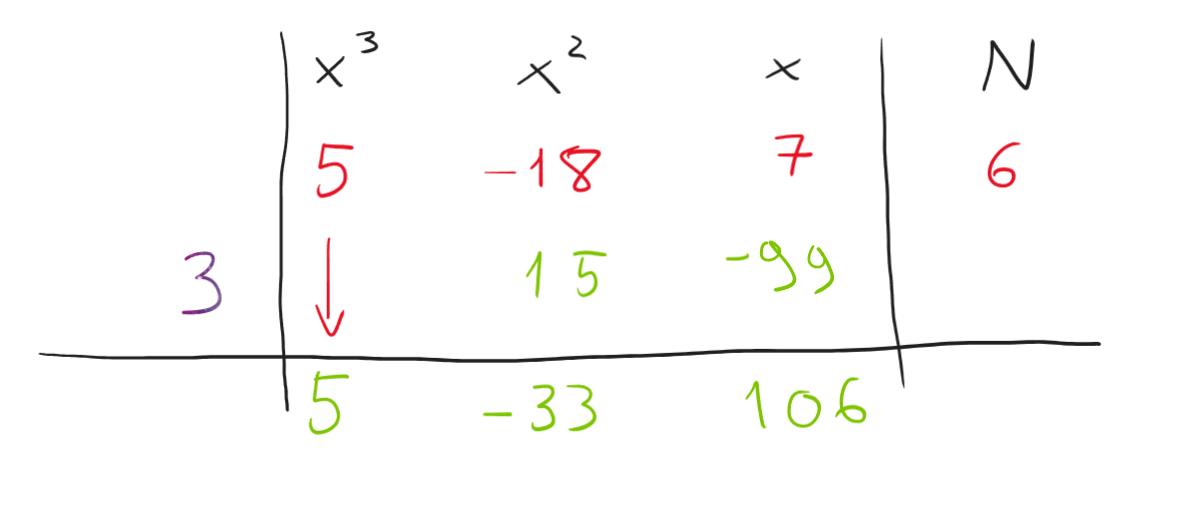
Ultimo giro, 106*3=318 che purtroppo sottratto a 6 non ci restituisce il nostro agognato zero!

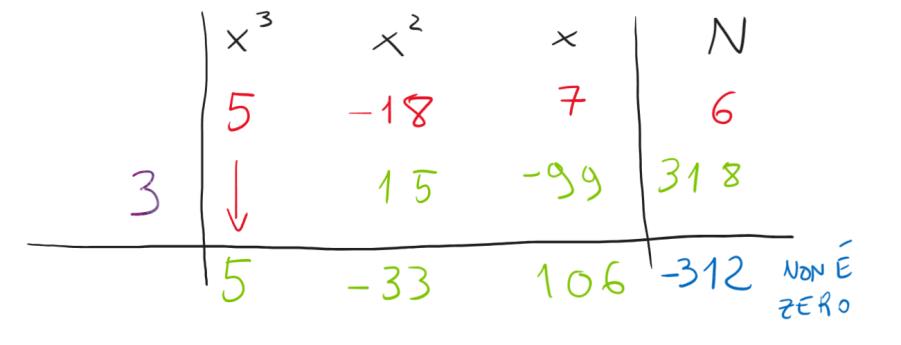
Un altro buco nell’acqua, ma ecco che possiamo già notare qualcosa. Aumentando il moltiplicatore da 2 a 3 abbiamo ottenuto come numero finale un numero in valore assoluto ancora più grande, passando da -120 a -312. Questo deve farci riflettere, probabilmente la soluzione la otterremo con un numero più piccolo del 2 che abbiamo scelto inizialmente. E se provassimo con -3?

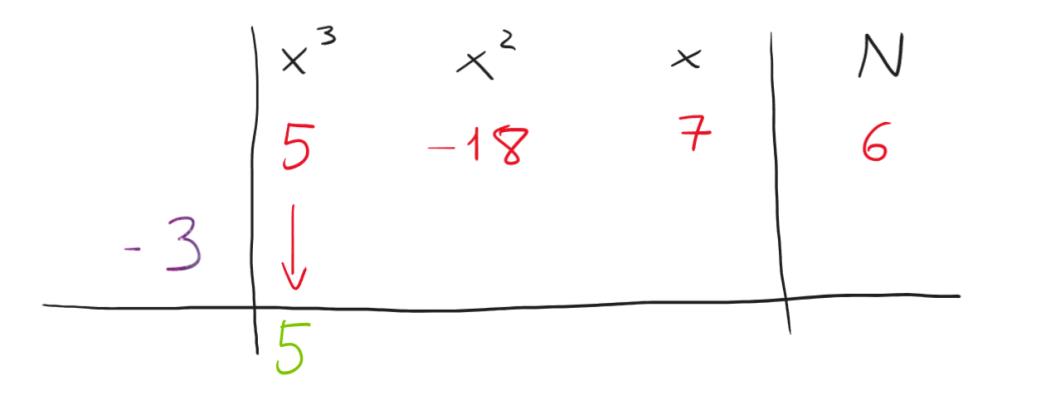
La situazione adesso è questa, abbiamo -3 come moltiplicatore. Facciamo i nostri calcoli, come abbiamo imparato negli esempi precedenti:  -3*5=-15 da cui

-18-(-15)=-18+15=-3

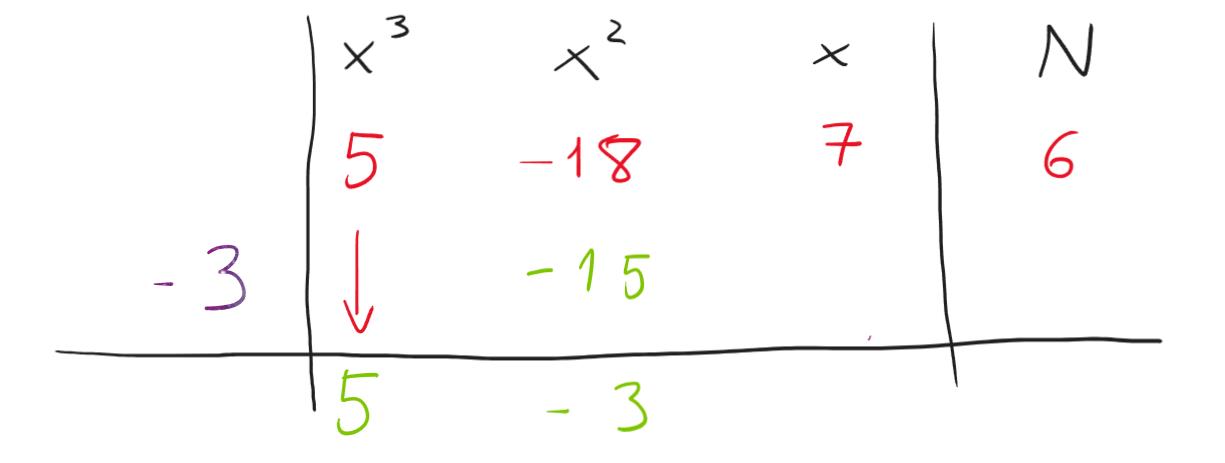
Pronti per un nuovo giro? -3*(-3)=9 da cui 7-9=-2

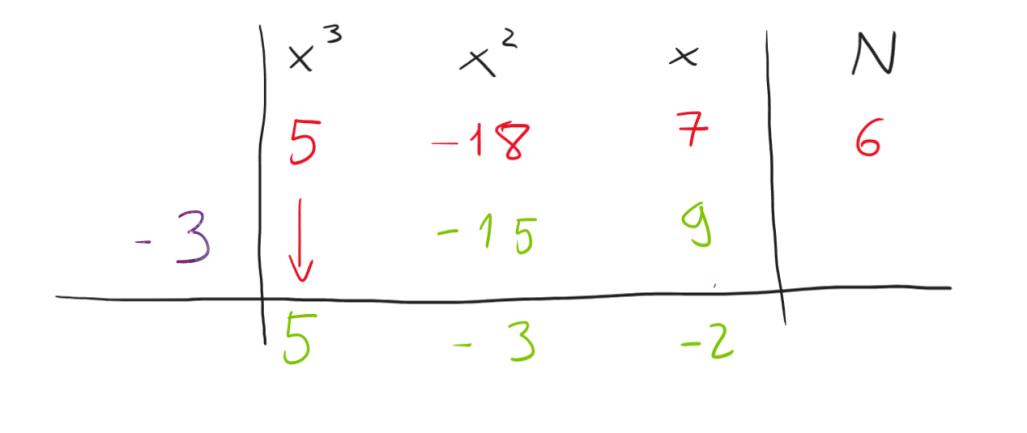
Questo sì che sembra promettente! Facciamo gli ultimi calcoli ora: -2*(-3)=6 e quindi 6-6=0

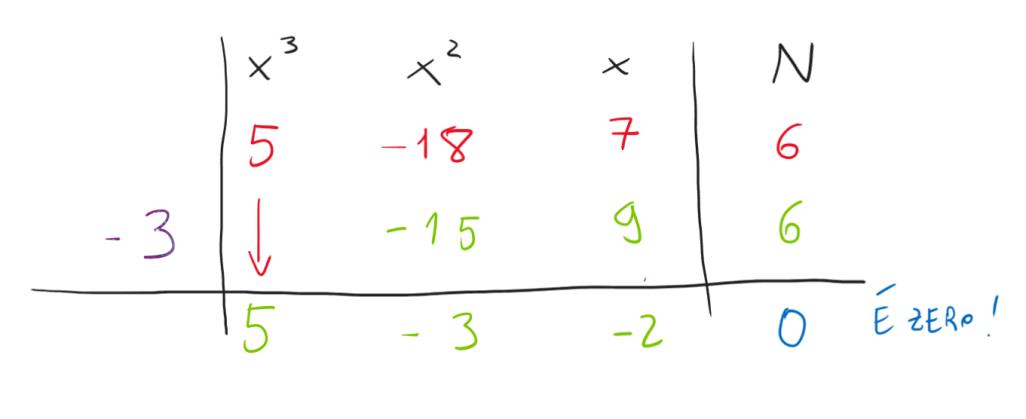
Ce l’abbiamo fatta! Abbiamo ottenuto zero nell’ultima casella, il metodo di Ruffini ha funzionato. Ma come interpretiamo ora questi risultati?

Niente di più facile, tenete sempre a mente qual era l’obiettivo iniziale, trovare divisore e quoziente della nostra divisione tra polinomi e finalmente ce li abbiamo di fronte.

Uno sarà nient’altro che x-3 (il nostro utilissimo moltiplicatore!) e l’altro lo comporremo utilizzando i coefficienti calcolati nella terza riga, ossia 5, -3 e -2, ma come?

Anche questo è facile, ogni coefficiente è stato inserito in una colonna relativa a una potenza delle incognite x, il nostro nuovo polinomio si comporrà quindi abbassando di un grado ciascuna di queste x.

Se quindi il 5 compare nella colonna relativa a  allora nel nuovo polinomio sarà il coefficiente del termine in  e così via per gli altri termini, se -3 è stato scritto nella colonna relativa a  allora sarà il coefficiente del termine in x nel nuovo polinomio, infine -2 sarà il nuovo termine noto.

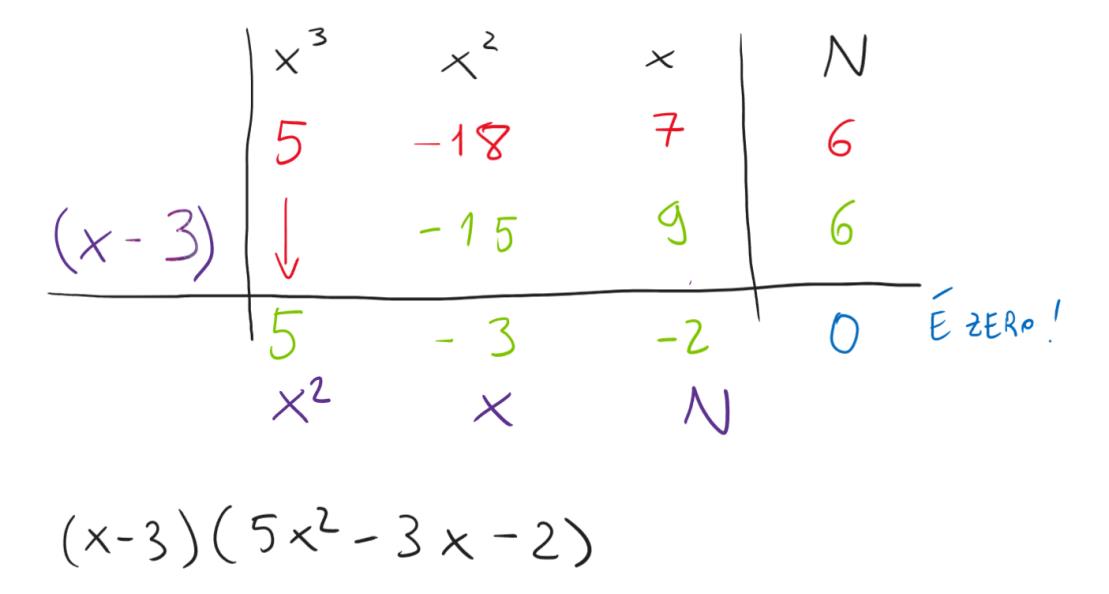
Ecco i nostri dividendo e quoziente della divisione

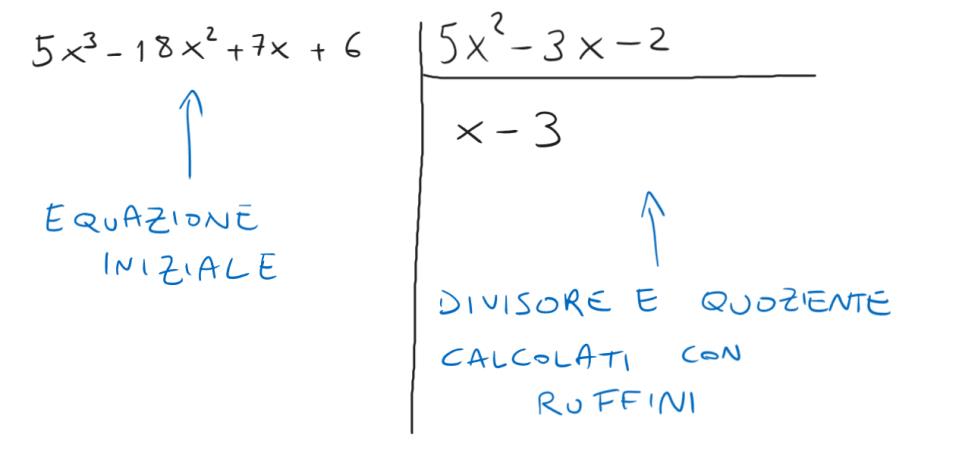
Finalmente possiamo risolvere la nostra equazione di terzo grado! La bestia brutta e cattiva

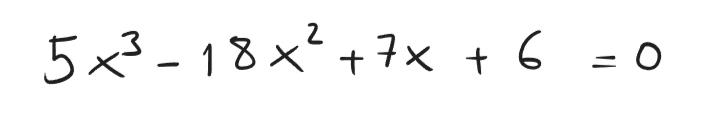
è stata ricondotta a due micetti docili docili

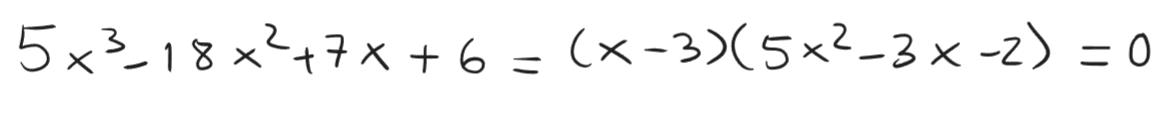
Da qui trovare le tre soluzioni dell’equazione di terzo grado è cosa facile, occorrerà risolvere separatamente l’equazione di primo grado e l’equazione di secondo grado, come di seguito

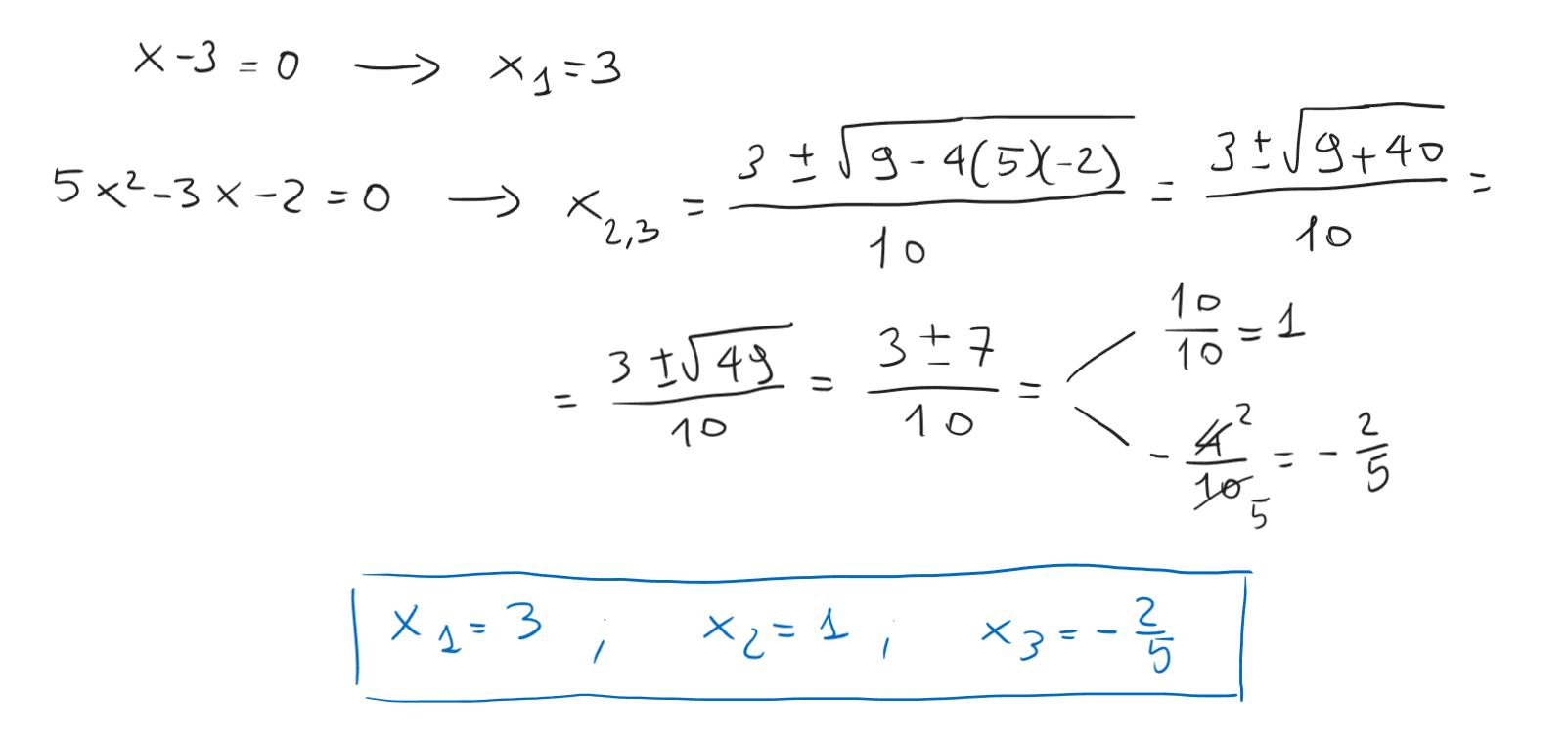
Siamo arrivati alla conclusione, spero che questo excursus possa aver chiarito le idee a qualcuno sul metodo di Ruffini.

In ogni caso, non lasciatevi mai scoraggiare dalle difficoltà, per quanto un problema possa sembrare complicato, se riuscirete a scomporlo in problemi più piccoli e più facilmente affrontabili, allora anche il mostro più temibile diventerà docile e questo vale sempre, non solo in matematica, ma per ogni problema della vita!