Distribuzione Binomiale: spiegazione con esempio numerico

Immaginiamo di fare un esperimento, o chiamiamolo test o anche prova, che possa dare due soli risultati, ad esempio successo o fallimento. Tale esperimento è chiamato processo di Bernoulli (Bernoulli trial in inglese).

Potrebbe, ad esempio, anche trattarsi del lancio di una moneta che, come sappiamo può dare due soli risultati, testa o croce, (potremmo assumere testa come successo e croce come fallimento). 

Eseguiamo questo esperimento di Bernoulli un certo numero di volte, consapevoli del fatto che i risultati (successo o fallimento) degli esperimenti sono completamente indipendenti dagli altri. Inoltre, consideriamo anche che la probabilità di un successo è costante e vale p (nel caso di fare testa con un lancio di moneta p=0.5 (o 50%) e questa probabilità sarà sempre la stessa ad ogni lancio) e che il fallimento ha ovviamente probabilità sempre costante e vale 1-p (essendo i risultati solo due, la somma delle loro probabilità deve dare uno):

p+(1-p)=1.

Consideriamo ora, come esperimento quello di fare 2 volte testa con 3 lanci di moneta, ogni lancio è indipendente dal precedente. 

Tutti i risultati possibili di questa prova che potremmo aspettarci sono:

TTT TTC TCC CCC CTT CCT CTC TCT  cioè 2^3=8 combinazioni possibili

T=testa e C=croce

Ovviamente, siamo interessati ad avere 2 teste nei tre lanci e quindi avremo solo 3 possibili combinazioni interessanti per noi: TTC CTT e TCT.  

Il fatto che le combinazioni con due teste sono 3 poteva calcolarsi anche utilizzando la nota formula del calcolo combinatorio:

dato un insieme di cardinalità n (nel nostro caso 3 lanci di monete), i sottoinsiemi di cardinalità x cioe' le combinazioni possibili dei tre lanci dove figurano 2 teste e due croci e' :

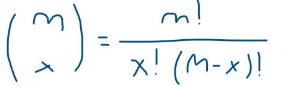
La probabilita di avere 2 teste con tre lanci di una moneta è:

P(T)*P(T)*P(C)=p*p*(1-p)=0.5*0.5*(1-0.5)=0.5^3=0.125 o se vogliamo 12.5%

Tuttavia, ci sono tre possibili modi con cui questa combinazione di 2 teste e una croce può verificarsi, quindi, la probabilita di fare 2 teste con 3 lanci di moneta è 0.125*3=0.375 o 37.5%.

Arrivati fino a questo punto, possiamo dire che

considerato un esperimento che consiste di un certo numero n di processi o prove di Bernoulli tali che:

1. le prove sono tra loro indipendenti

2. ogni prova ha solo due possibili risultati (successo o fallimento)

3. la probabilità di successo di ogni prova vale p e rimane costante

la variabile aleatoria Y che mi dice il numero di esperimenti per i quali sono riuscito nello scopo prefissato (nell esempio precedente, il numero di volte che ottengo 2 teste su tre lanci) è una variabile aleatoria binomiale, la cui funzione di probabilità è

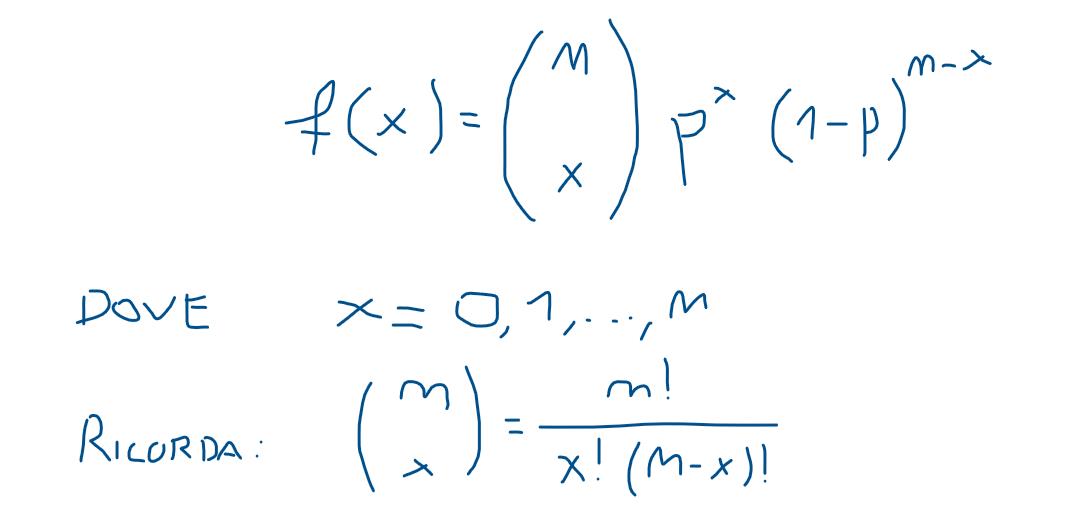
nell esempio precedente, n vale 3 (numero di lanci di moneta), x vale 2 (2 teste su 3 lanci appunto) e p vale 50% o 0.5.

Sostituendo i valori nella formula si ottiene la probabilita di ottenere 2 teste con tre lanci di moneta, esattamente il valore 37.5%.

Nota inoltre che tale distribuzione di probabilità è discreta cioè definita su un insieme finito o numerabile.

Esempi tipici di variabili che seguono una distribuzione binomiale sono:

fare 2 teste con tre lanci di moneta

fare 3 volte 6 con sei lanci di dado

numero di femmine su 20 nascite

numero di bits errati su 10 bits trasmessi

numero di campioni contenenti inquinanti su 100 prelievi

etc....

ciao e buono studio!