- Blog
- Matematica
- Mappa concettuale per lo studio di funz...
Mappa concettuale per lo studio di funzione
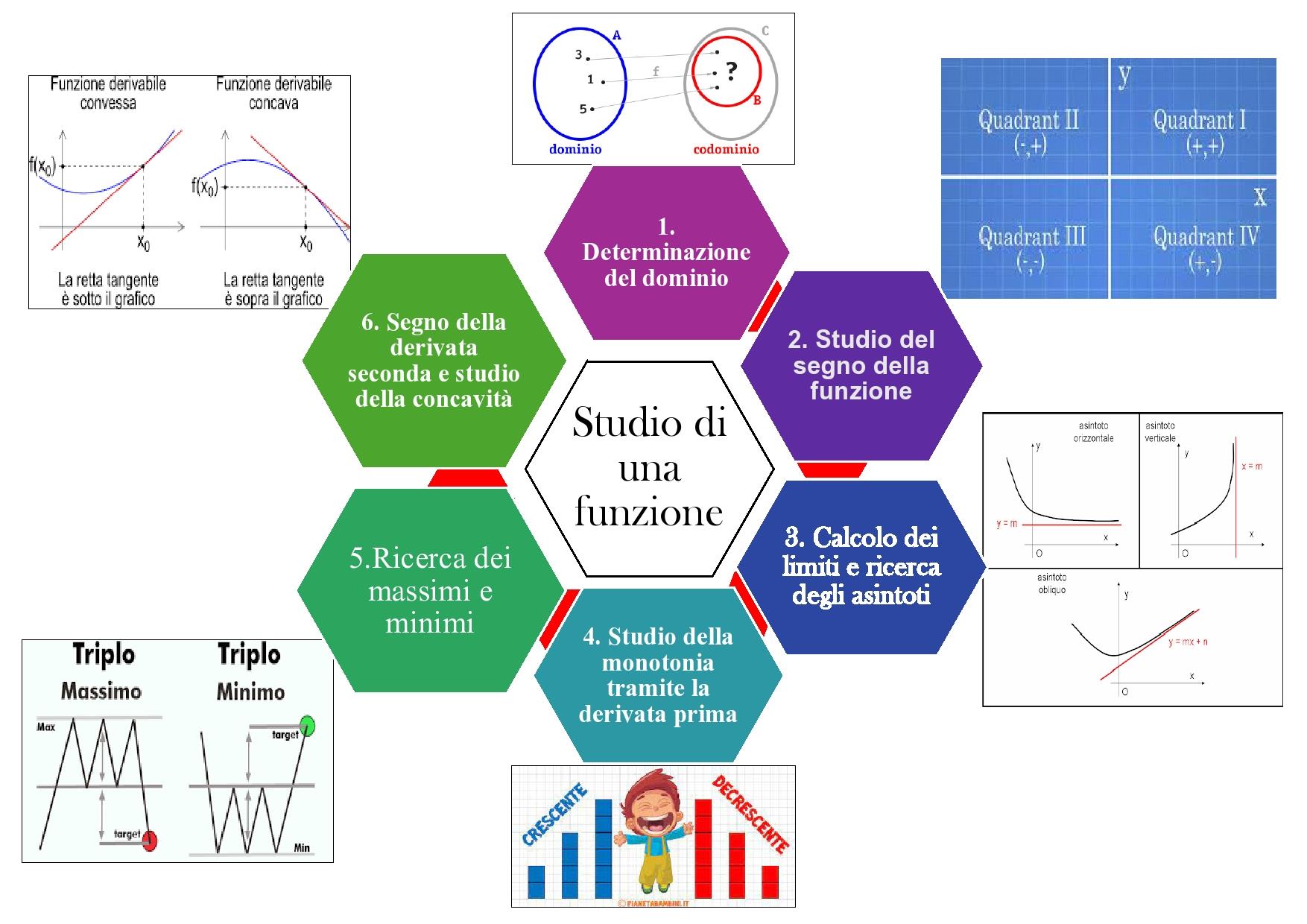
📚 Mappa concettuale per lo studio delle funzioni
Durante la mia esperienza come tutor universitario per studenti con Disturbi Specifici dell’Apprendimento (DSA), ho progettato una mappa concettuale per semplificare e organizzare i concetti fondamentali dello studio delle funzioni. Questo strumento è stato creato per fornire una panoramica chiara e accessibile, facilitando la comprensione e l’apprendimento attraverso un approccio visivo e schematico.
Lo studio delle funzioni è una delle competenze più importanti in matematica, ma può essere complesso per molti studenti, soprattutto per coloro che richiedono un metodo di insegnamento su misura. Per questo motivo, la mappa concettuale che ho sviluppato si articola in sei step chiave, ognuno pensato per affrontare le principali sfide in modo chiaro e graduale.
Prova ripetizioni di matematicahttps
📌Nota importante
Questa mappa non rappresenta un’analisi esaustiva di tutte le nozioni relative alle funzioni, ma piuttosto un insieme di elementi essenziali per ricordare la struttura di studio e facilitare l’apprendimento.
11. Determinazione del dominio
Il primo passo nello studio di una funzione è identificare il suo dominio, cioè l’insieme di x per i quali la funzione è definita. Ciò include l’analisi di eventuali restrizioni, come i denominatori nulli o radici quadrate di numeri negativi. La comprensione del dominio fornisce una base per tutti i passaggi successivi.
22. Analisi del segno della funzione
Il secondo passo consiste nell’analizzare il segno della funzione, determinando dove è positivo, negativo o nullo. Questo comporta:
· la risoluzione delle disequazioni f(x) > 0, f(x) < 0
· la risoluzione dell’equazione f(x) = 0, che consente di individuare i punti in cui la curva interseca l’asse x.
· Il calcolo f(0), per individuare il punto di intersezione della funzione con l’asse y.
Infine, si procede allo studio della parità della funzione:
· Se f(−x) = f(x), la funzione è pari (simmetrica rispetto all’asse y)
· Se f(−x) = − f(x), la funzione è dispari (simmetrica rispetto all’origine).
Questo consente di individuare eventuali proprietà di simmetria che facilitano l’analisi e la rappresentazione grafica.Questa fase è essenziale per comprendere il grafico e il comportamento della funzione.
33. Calcolo dei limiti e identificazione di eventuali asintoti
Il terzo passaggio prevede il calcolo dei limiti della funzione, sia agli estremi del dominio che nei punti critici. Questo aiuta a identificare eventuali asintoti verticali, orizzontali o obliqui, che sono fondamentali per capire come si comporta la funzione all’infinito o vicino a valori specifici. Inoltre, si può includere lo studio della continuità della funzione per determinare eventuali punti di discontinuità.
44. Studiare la monotonia usando la derivata
Dopo aver analizzato il dominio e gli asintoti, il passo successivo è lo studio della monotonia. Questo viene fatto calcolando la derivata prima della funzione f’(x) per determinare:
· Dove f’(x) > 0 , la funzione è crescente;
· Dove f’(x) < 0 , funzione è decrescente,
· Dove f '(x) = 0, funzione è costante.
Questa analisi aiuta a identificare gli intervalli di crescita, decrescita o costanza della funzione, elementi essenziali per analizzare il suo comportamento complessivo.
55. Identificazione di massimi e minimi.
Utilizzando l’analisi della derivata prima, è possibile identificare i punti critici della funzione, dove f’(x)=0 o è indefinito. Questi punti vengono ulteriormente analizzati per determinare se rappresentano massimi o minimi locali, che sono cruciali per rappresentare graficamente la funzione.
66. Analisi della derivata seconda
Il passaggio finale prevede il calcolo della derivata seconda f”(x), che viene utilizzata per analizzare la concavità della funzione e identificare possibili punti di flesso.
· Se f”(x) > 0, la funzione è convessa (rivolta verso l’alto).
· Se f”(x) < 0, la funzione è concava (rivolta verso il basso).
· Se f”(x) = 0 in un punto, potrebbe trattarsi di un punto di flesso, che richiede ulteriori verifiche.
Questo passaggio completa l’analisi della funzione e fornisce le informazioni necessarie per la sua rappresentazione grafica.
🎯 Perché questa mappa è utile ?
Questa mappa concettuale è progettata per rendere il processo di studio più chiaro e organizzato. Dividerlo in passaggi semplici e progressivi aiuta a ridurre la complessità percepita, migliorando la comprensione generale. È particolarmente utile per gli studenti con DSA per la sua struttura visiva e chiarezza, ma può anche essere un aiuto prezioso per chiunque voglia avvicinarsi allo studio delle funzioni in modo metodico ed efficace.
📖 Vuoi sapere di più o hai bisogno di aiuto?
Se sei interessato a utilizzare questa mappa per i tuoi studi o hai bisogno di supporto nello studio delle funzioni, non esitare a contattarmi! 😊