- Blog
- Matematica
- Come svolgere funzioni in esercizi di m...
Come affrontare le funzioni matematiche in serenità
Sebbene temuta da liceali e universitari la matematica è da sempre più semplice di quello che sembra.
Alla base di un corretto approccio alla disciplina è opportuna la comprensione logica dell'argomento, al giorno d'oggi i ragazzi ripetono in maniera meccanica esercizi ed esercizi fissando il metodo ma senza comprendere a fondo il significato di quei passaggi svolti svariate volte.
Un esempio di tutto cio è l'approccio che viene propoposto nello studio delle funzioni: esponenziali, logaritmi, valore assoluto, tangenti e tante altre...
Queste funzioni spaventano gli studenti che affrontandole nella maniera sbagliata si trovano in grande difficoltà.
In questo articolo voglio promuovere un approccio logico all'argomento cercando di comprendere prima il significato di una data espressione, per poi passare agli immancabili calcoli.
Vediamo quindi come ragionare e come calcolare davanti ad una funzione matematica.
Per prima cosa ci troveremo un espressione del tipo y=f(x), dove viene stabilità una dipendenza tra una certa variabile y e una certa variabile x secondo un certo funzionale. Vediamo quindi un esempio per essere più efficaci, consideriamo la funzione y=1/x. La funzione in questione assegna una relazione tra la y e la x, questo vuol dire che al variare della nostra variabile indipendente x possiamo assegnare dei valori alla variabile dipendente y. Quello che ci occorre per prima cosa e definire le condizioni per cui l'espressione scritta ha significato matematico. Questo perchè nel nostro caso y=1/x, non tutti i valori di x possono essere considerati validi, sappiamo infatti che non è possibile effettuare una divisione per 0 e quindi dobbiamo escludere lo zero dal dominio della funzione.
Una volta individuato il dominio con un approccio logico alla funzione in questione, vogliamo provare a graficarla, senza ricorrere ancora allo studio di funzione e ai suoi passaggi meccanici.
La maniera più semplice per fare ciò è andare a sostituire dei valori di x all'interno dell'equazione calcolando il corrispettivo valore di y. Diamo quindi un'occhiata all'immagine: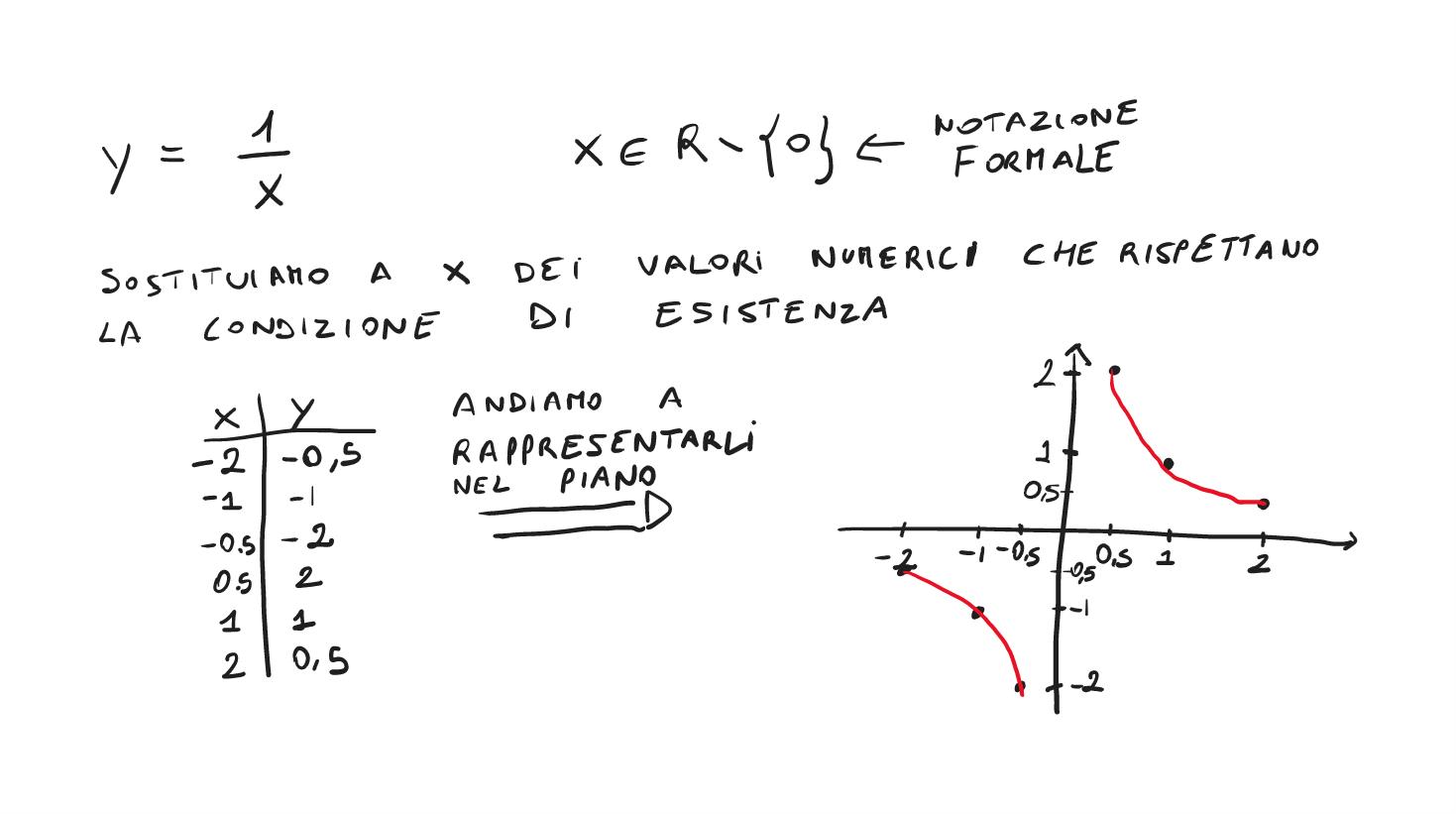
Una volta arrivati a questo punto possiamo banalmente collegare i punti ottenuti garantendoci cosi quella che è una bozza della nostra funzione effettiva.
Ampliando il numero dei punti possiamo ottenere una bozza sempre più precisa, e cosi facendo possiamo garantirci una comprensione intuitiva della funzione che abbiamo davanti.
L'approccio proposto a mio giudizio risulta essere fondamentale per lo studente, in quanto una volta compreso 'il senso' della funzione può poi procedere in maniera più sicura e consapevole allo svolgimento dell'esercizio in questione. Vediamo quindi qualche altro esempio nelle immagini seguenti:
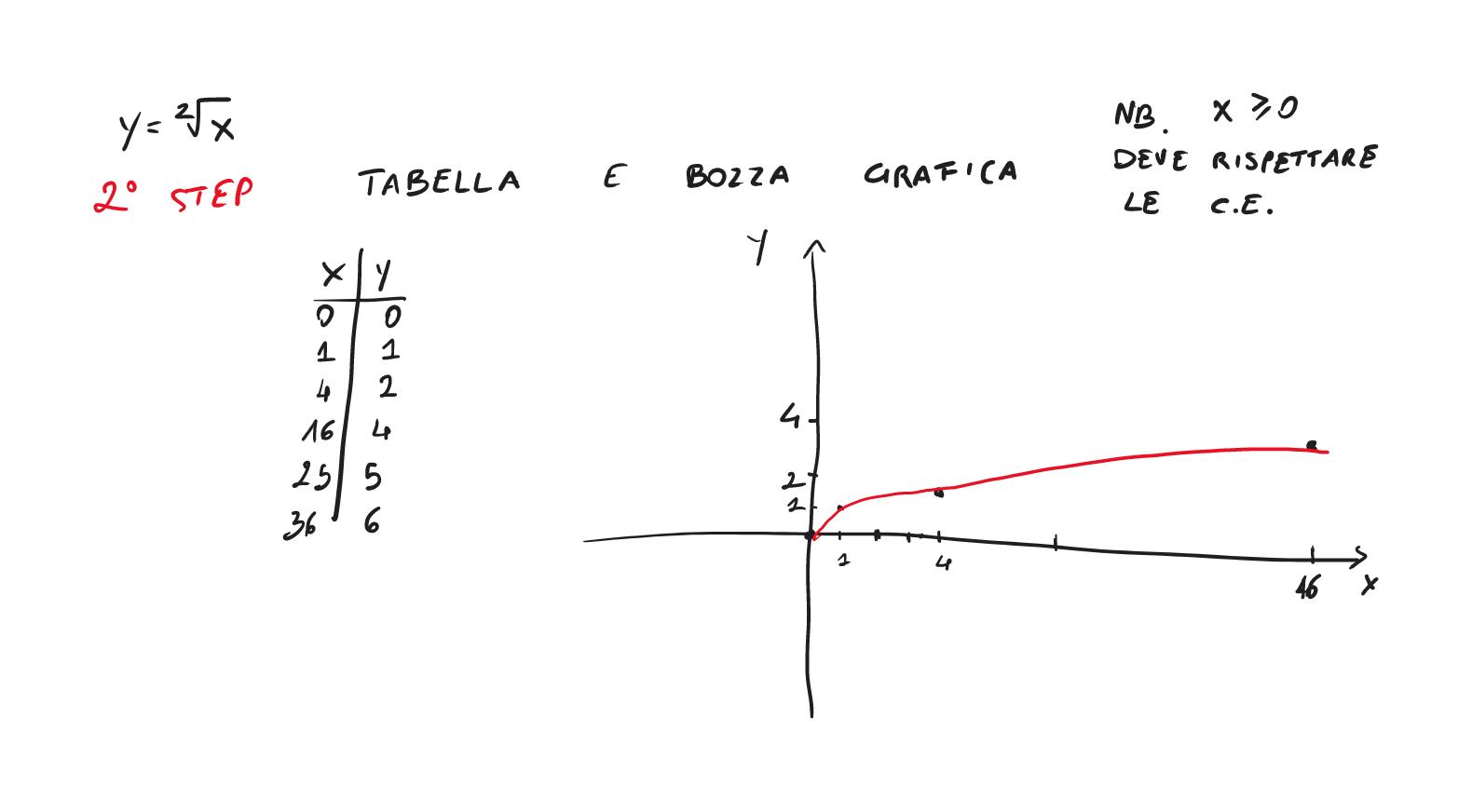
Come possiamo notare dai due esempi indicati l'approccio vincente parte dal farsi molte domande cercando di comprendere il perchè di ogni regola, ragionando sull'esercizio in primis, per poi applicare le metodologie risolutive.
Ovviamente, i due esempi proposti risultano essere banali, è quindi bene non soffermarsi sulle specifiche funzioni indicate in queste ripetizioni di matematica, ma cogliere il significato più generale dei consigli proposti, ovvero di basarsi sul ragionamento, cosa che molte volte viene accantonata dalle metodogie meccaniche che vengono proposte allo studente.


