Risoluzione di equazioni di terzo grado: metodi e esempi

Le equazioni di terzo grado sono equazioni polinomiali il cui grado massimo della variabile è 3, si presentano nella forma: ax³ + bx² + cx + d = 0 in cui x è la variabile incognita e i coefficienti numerici sono indicati da a,b,c,d, essendo un’equazione di terzo grado al massimo si possono ottenere 3 radici, ovvero 3 soluzioni.

Per risolvere queste equazioni è necessario scomporre i polinomi in modo da ottenere delle equazioni di secondo grado che possono essere risolte tramite la formula nota.

·         RACCOGLIMENTO TOTALE o PARZIALE

Per ottenere un’equazione di secondo grado si può procedere svolgendo un raccoglimento parziale o totale in modo da trovare una radice e successivamente risolvere l’equazione di secondo grado.

Esempio di raccoglimento TOTALE

presa l’equazione di III grado x³ + 6x² - 12x = 0

si può raccogliere la x ottenendo x ( x² + 6x – 12 ) = 0

da cui si ottiene una prima radice pari a x = 0

successivamente si risolve l’equazione di secondo grado ( x² + 6x – 12 ) = 0

·         RUFFINI

Un altro metodo per risolvere le equazioni di terzo grado è quello di usare il teorema di RUFFINI che permette di scomporre polinomi di qualsiasi grado, nel caso di polinomi di terzo grado permette di ottenere polinomi di secondo grado.

Per prima cosa è necessario trovare un valore di x tale che la somma algebrica del polinomio sia pari a zero.

Presa come esempio l’equazione 3x³ + 2x² - 6x - 20 = 0  

Bisogna trovare un numero da sostituire all’incognita x in modo che la somma sia uguale a 0. In questo caso il numero che annulla il polinomio è 2

Ovvero 3x2³ + 2x2² - 6x2 – 20 = 0

Effettuando le moltiplicazioni 24 + 8 – 12 – 20 = 0  la somma del polinomio è 0

Perciò x = 2  è una delle radici

Una volta trovata la radice bisogna creare la griglia ponendo sulla riga in alto tutti i coefficienti del polinomio ( se per esempio il fattore con x² non è presente allora al posto di questo coefficiente si inserisce lo zero).

In basso a sinistra si inserisce il valore dello zero del polinomio trovato precedentemente, in questo caso 2

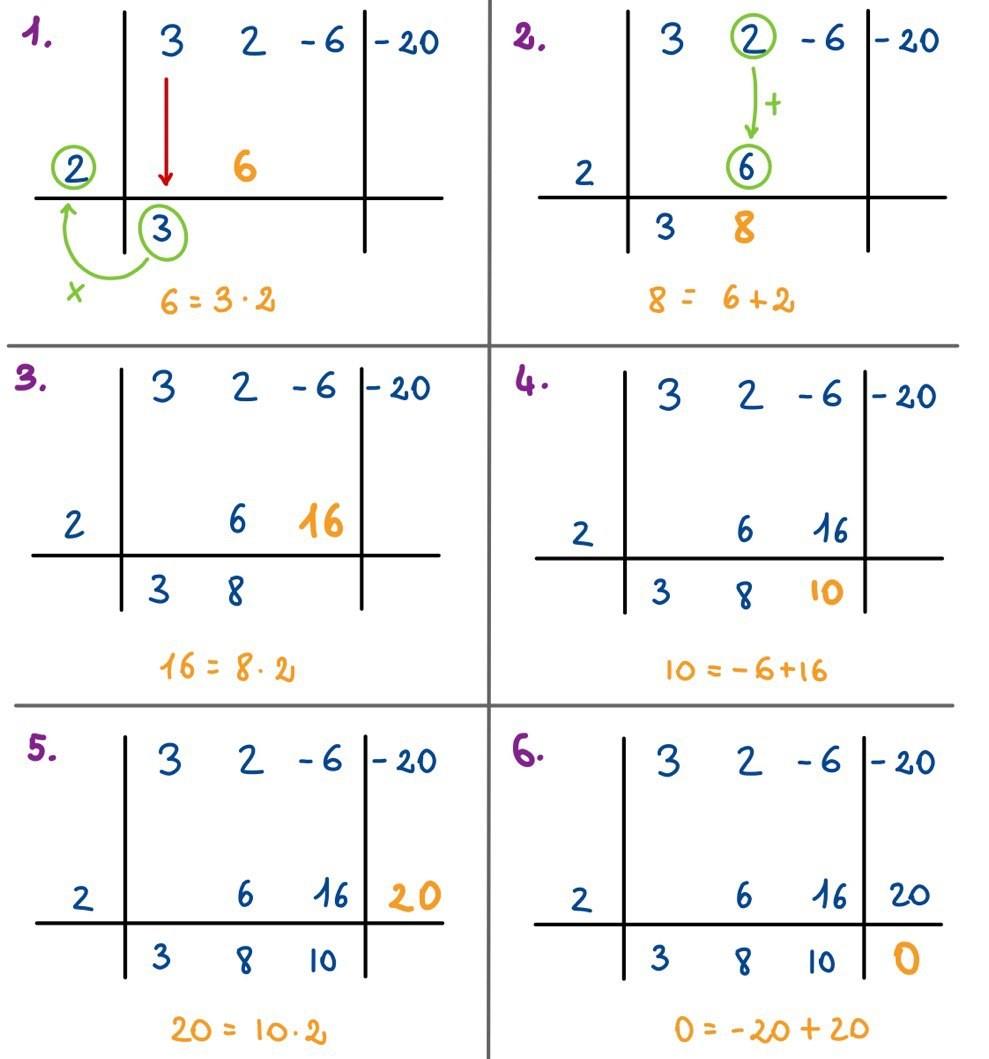
Il primo coefficiente (quello di grado più alto si riscrive in basso), nel caso del nostro esempio si riscriverà il  3 questo numero si moltiplica per il valore della radice e il numero ottenuto (ovvero 6 ) si riscrive sopra la riga orizzontale nella seconda colonna.

Si sommano quindi i due valori della seconda colonna (2 + 6 = 8) e il risultato si riporta sotto la riga orizzontale, la somma ottenuta si moltiplica per la radice (8 x 2 = 16) e il risultato si inserisce nella terza colonna sopra la riga orizzontale e si sommano i valori di questa colonna (- 6 + 16 = 10).

Il valore 10 si moltiplica per la radice 2 e il risultato 20 si inserisce nella quarta colonna, a questo punto ancora una volta si effettua la somma dei coefficienti della colonna (- 20 + 20 = 0)

Se i calcoli sono giusti il resto finale deve essere pari a 0.

I coefficienti della terza riga presi in ordine restituiscono i coefficienti dell’equazione di secondo grado ovvero 3x² + 8x + 10 = 0   perciò l’equazione di terzo grado può essere riscritta come la moltiplicazione tra l’equazione di secondo grado e la radice trovata in precedenza.

Considerando l’esempio in esame si ha quindi (3x² + 8x + 10 = 0) ( x – 2 ) = 0

Una radice è quella calcolata prima pari a x = 2 le altre devono essere trovate usando la formula nota.

(tutti i passaggi sono riportati nella foto)