Cos'è la distribuzione binomiale? (università o azienda)

Questo post continua il discorso introdotto nel post Cos'è la distribuzione binomiale? Esercizi e soluzioni (scuola secondaria).

Qui vediamo alcune applicazioni che richiedono conoscenze normalmente acquisite in corsi universitari di analisi, probabilità e statistica, oppure con l'esperienza in azienda.

Lo scopo è duplice. Da una parte si vuole mostrare l'importanza della distribuzione binomiale a chi sta affrontando un percorso di studio universitario. Dall'altra vogliamo far conoscere agli esperti di una delle applicazioni citate l'esistenza anche delle altre. Chi incontra la binomiale in un contesto specifico è improbabile che sia a conoscenza degli altri, il grande pregio della Matematica è proprio quello di mettere in comunicazione (formale e non ambigua) esperti lontani nel tempo e nello spazio, così che tutti possano trarne beneficio.

Naturalmente, possiamo solo accennare alle idee ed ai risultati che citiamo. Il lettore è invitato a seguire i riferimenti per approfondire.

Il lancio di una monenta è truccato

Fra gli esempi citati nel post precedente, il lancio di una moneta è sicuramente quello paradigmatico. È sorprendente quindi osservare che lanciare una moneta con il pollice facendola roteare in aria introduce una disparità nelle probabilità degli eventi; in particolare l'evento "la moneta si ferma con in alto la stessa faccia che aveva prima del lancio" ha probabilità leggermente maggiore dell'evento "la moneta si ferma con in alto l'altra faccia rispetto a quella che aveva prima del lancio".

Una prima spiegazione rigorosa di questo fenomeno è stata proposta nel paper Dynamical Bias in the Coin Toss. Nel seguito chiameremo il modello analizzato D-H-M.

Solo recentemente è arrivata la verifica sperimentale di questo fatto basata su 350757 lanci e pubblicata nel paper Fair coins tend to land on the same side they started: Evidence from 350,757 flips. Usando le parole degli autori:

the standard model of coin flipping was extended by Diaconis, Holmes, and Montgomery (D-H-M) who proposed that when people flip a ordinary coin, they introduce a small degree of ‘precession’ or wobble—a change in the direction of the axis of rotation throughout the coin’s trajectory. According to the D-H-M model, precession causes the coin to spend more time in the air with the initial side facing up. Consequently, the coin has a higher chance of landing on the same side as it started (i.e., ‘same-side bias’)

È interessante notare il metodo, che rientra nell'open science, seguito: prima si impostano gli esperimenti e si definiscono dettagli minuti almeno di una parte delle investigazioni (fra questi anche gli obbiettivi), poi si avvia la fase sperimentale. Anche se gli obbiettivi non sono raggiunti rimane traccia, ed esistono riviste scientifiche che pubblicano anche risultati negativi ottenuti con questo livello di rigore.Giusto per curiosità, leggiamo che: 

Pr(same side) = 0.508, 95% CI [0.506, 0.509]. [...] In addition, the data show no trace of a heads-tails bias: Pr(heads) = 0.500, 95% CI [0.498, 0.502].

Leggiamo anche che alcuni (mate)maghi riescono a sfruttare questo fatto per indirizzare gli esiti dei lanci. Fra le numerose analisi svolte nel paper, il ruolo ricoperto dalla distribuzione binomiale è quello da protagonista. 

Generalized Linear Model

Il modello D-H-M citato prima è un modello fisico che parte dai first principles, cioè sfrutta assunzioni fondamentali (in questo caso della fisica newtoniana) e descrive nel dettagli l'interazione fra vari componenti del sistema (nell'esempio, il dito e la moneta). Questo tipo di modello viene chiamato white box perché possiamo capirne i meccanismi interni; in particolare le relazioni fra gli inputs e gli outputs del modello sono interpretabili (e l'interpretazione è giustificata dalla dettagliata conoscenza dei meccanismi interni).

Concentriamoci adesso su un tipo di modello molto diverso, un modello black box di cui non possiamo studiare il meccanismo. Analizzando però gli inputs e gli outputs possiamo interpretare almeno parzialmente le relazioni. Ad esempio, il contesto dell'applicazione ci dice che al crescere di una variabile indipendente cresce anche una variabile dipendente. L'esempio più semplice che realizza la dipendenza descritta è il modello lineare, ma questo mal si adatta a diverse situazioni che si incontrano in contesti aziendali, di scienze della vita oppure ingegneristiche. Non è sempre possibile o utile studiare i dettagli di un prodotto/essere vivente/artefatto, oppure comprendere tutti i dettagli delle interazioni fra artefatti, oppure il successo di un prodotto in diversi mercati, fra un essere vivente e l'ecosistema in cui si sviluppa.  

Fra le varie generalizzazioni del modello lineare, è di grande utilità pratica la binomial generalized linear model with logit link function, dove la proporzione di successi rispetto al numero di tentativi può essere collegata ad un modello lineare. Dettagli sono facilmente rintracciabili -- ad esempio -- nei manuali di statistical learning. 

Albero binomiale e finanza

Uno degli strumenti finanziari più utilizzati, in particolare perché può determinare investimenti a basso rischio con buoni rendimenti, è l'opzione su azione. In generale citando il sito della borsa italiana:

le opzioni sono strumenti finanziari il cui valore non è autonomo ma deriva dal prezzo di una attività sottostante di varia natura (reale come nel caso di materie prime quali grano, oro, petrolio, ecc. , oppure finanziaria come nel caso di azioni, obbligazioni, tassi di cambio, indici, ecc.). Il termine “derivato” indica questa dipendenza.

Qui naturalmente affronteremo l'argomento semplificando molto (seguendo il modello di Cox, Ross e Rubinstein del 1979). L'idea è che il valore di un bene (ad esempio una azione in borsa) varia nel tempo in modo casuale ed è possibile acquistare o vendere oggi la possibilità di comprare o vendere dopo un certo periodo il bene ad un certo prezzo (strike price). Oggi compriamo 'la possibilità', cioè l'opzione; il sottostante in questo caso è l'azione di borsa. Ci chiediamo: quanto vale oggi l'opzione? Questa informazione ci permette di contrattare consapevolmente sui mercati specializzati nella compravendita di opzioni.

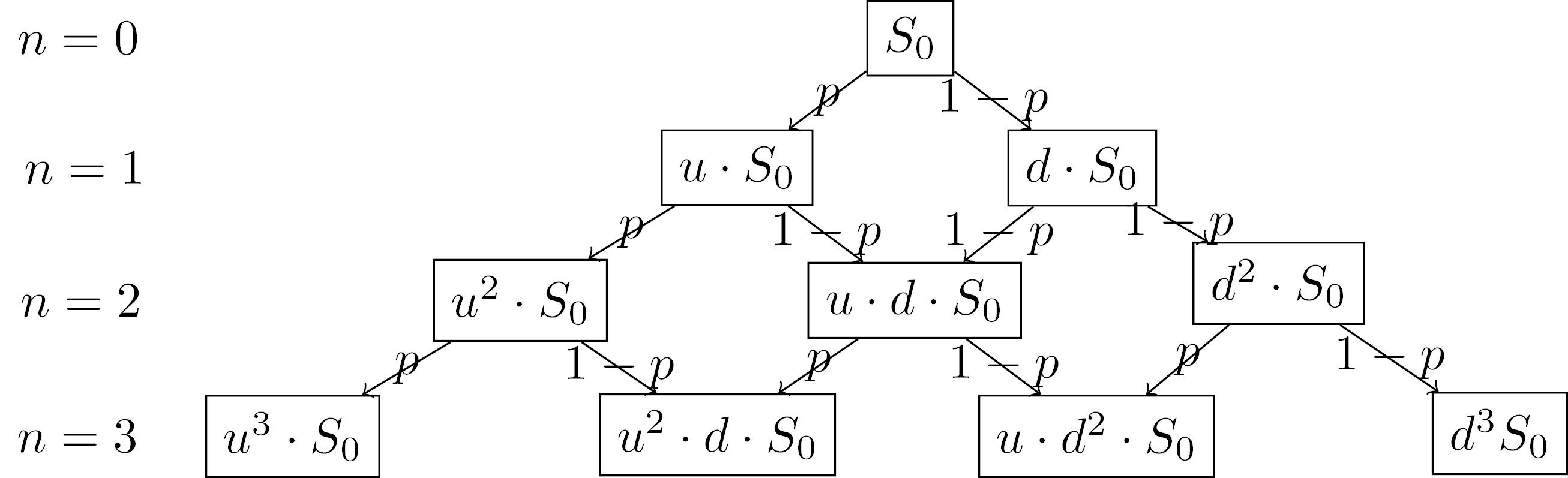
Per semplicità consideriamo intervalli di tempo Dt molto piccoli in cui il valore del sottostante S (in inglese security) può aumentare di un fattore u (up) con probabilità p oppure diminuire con probabilità 1-p di un fattore d (down). Come scegliere i parametri Dt, p, u e d dipende da molti fattori. Dopo un periodo di n intervalli Dt il valore del sottostante ha distribuzione binomiale. Possiamo visualizzare l'andamento del valore del sottostante riprendiamo l'albero binomiale visto nel precedente post, questa volta però i nodi non riportano il numero di teste e di croci con n lanci di monete ma il valore del sottostante.

Arrivati alle foglie dell'albero, possiamo valutare l'opzione a seconda che il valore del sottostante siamo maggiore o minore dello strike price, e poi procedere a ritroso nell'albero per propagare il prezzo dell'opzione fino alla radice. Otterremo così il valore dell'opzione oggi.

Reliability di NVP

Qui consideriamo la probabilità di successo p, parametro reale fra 0 ed 1. Possiamo scrivere la Reliability dell'NVP come approssimazione di una funzione di voto g con polinomi di Bernstein di grado n=2f+1, dove f è il numero di guasti che possiamo tollerare. L'esempio classico è con maggioranza semplice che corrisponde a:

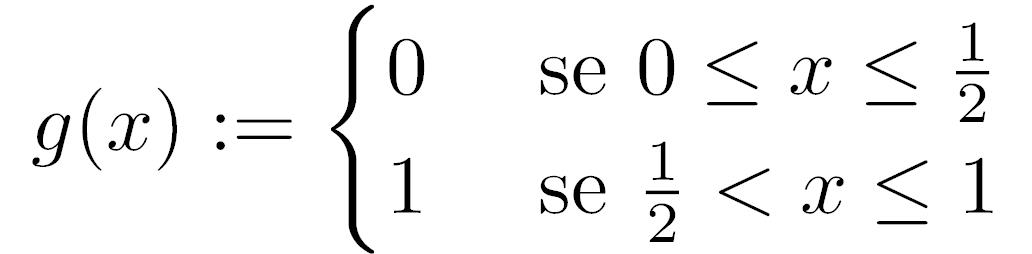
e la Reliability vista nel precedente post possiamo scriverla come:

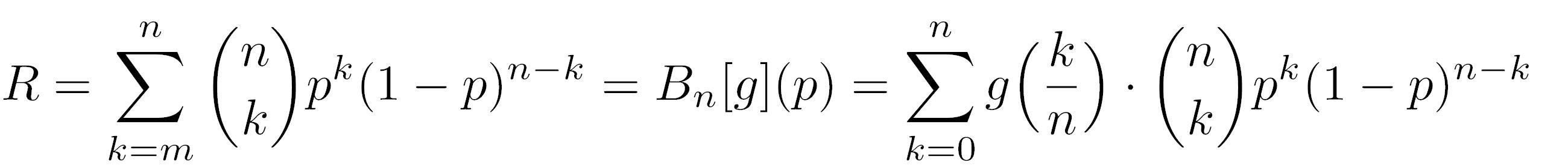
In alcuni casi altre maggioranze (ad esempio la maggioranza qualificata) vengono utilizzate, cambiando quindi la definizione di g.

Dimostrazione teorema di Weierstrass con la distribuzione binomiale

Possiamo lavorare con polinomi di Bernstein e la disuguagianza di Chebishev  per dimostrare il teorema di Weierstrass, una delle bestie nere del corso di analisi.

Questa osservazione ci mostra la grande utilità della distribuzione binomiale non solo per applicazioni direttamente pratiche ma anche come strumento nelle dimostrazioni astratte. Indirettamente, visto che dal teorema di Weierstrass a cascata dipendono risultati fondamentali di analisi, la distribuzione binomiale influenza quindi molte applicazioni.

Altro esempio di questo tipo è la dimostrazione basata su approssimazione con polinomi di Bernstein del teorema limite centrale proposta in (PhD thesis di Patricia Mehron Garmirian del 2013)

Probability of failure on demand (pfd)

Nel post precedente, come esercizio, abbiamo visto come calcolare il numero di tests da svolgere senza insuccessi per avere una certa confidenza che la pfd sia più piccola di una certa soglia, imposta di solito da qualche standard internazionale. Una derivazione formale è richiamata in A conservative confidence bound for the probability of failure on demand of a software-based system based on failure-free tests of its components. In questo paper è offerta anche un'analisi molto interessante che, ancora una volta, mette in evidenza la distinzione fra modello back box e modello white box. Nell'analisi classica infatti la funzione critica è considerata black box, se tuttavia conosciamo i dettagli dell'architettura della sua implementazione (un modello white box) possiamo cercare di ridurre il numero di tests, e dunque rispariare notevoli risorse. Gli stessi autori hanno poi presentato l'ottimizzazione in Optimising the reliability that can be claimed for a software-based system based on failure-free tests of its components.