I teoremi del seno e del coseno: esempi grafici
I teoremi del seno e del coseno sono delle relazioni geometriche utili per determinare la lunghezza dei lati e l’ampiezza degli angoli in un triangolo.
Teorema del seno
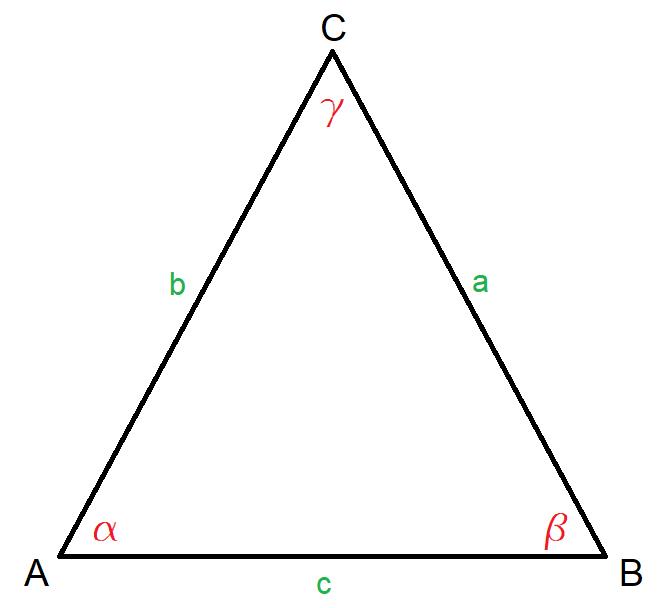
Consideriamo un triangolo qualsiasi dove abbiamo:
· a, b e c che rappresentano la lunghezza dei lati
· a, b e g che rappresentano gli angoli opposti alle lunghezze a, b e c
Definizione: in un triangolo qualsiasi il rapporto tra la lunghezza di un lato ed il seno dell’angolo opposto è costante per tutti e tre i lati.
Esaminiamo meglio la definizione, se noi prendiamo il rapporto tra la lunghezza b e il seno dell’angolo opposto b otterremo un valore che possiamo definire con K (costante) un valore che non cambia, analogamente facendo il rapporto tra la lunghezza a e il seno dell’angolo opposto a otterremo lo stesso valore della costante K.
Quindi potremmo scrivere che:
· 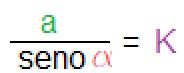
· 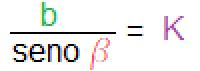
· 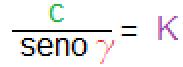
dove C avrà lo stesso valore in tutti e tre i casi, di conseguenza si potrebbe affermare che il rapporto tra la lunghezza a e il seno dell’angolo opposto a sarà uguale al rapporto tra la lunghezza b e il seno dell’angolo opposto b come sarà uguale anche al rapporto tra la lunghezza c e il seno dell’angolo opposto g. di conseguenza possiamo tranquillamente scrivere:
· 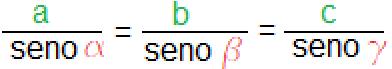
esempio
consideriamo di avere i seguenti dati della figura precedentemente esaminata: g=50°, b=60° ed infine a= 10 cm
per poter applicare il teorema dei seni, è necessario trovare l’incognita per poter svolgere l’esempio, di conseguenza si andrà a ricavare a che non è altro che la differenza tra la somma totale degli angoli di un triangolo e i suoi rispettivi due angoli a noi noti.
a= 180 -g -b = 180°–50°–60° = 70°
ora conosciamo i dati necessari per poter svolgere il teorema dei seni
conosciamo tutti gli angolo e una lunghezza, di conseguenza si andrà a ricavare una delle due incognite mancanti, b e c
· 
Si andrà ad isolare l’incognita da trovare, portando tutti i valori conosciti nell’altra parte (se è al denominatore, passerà al numeratore moltiplicando il valore esistente)
· 
Sostituendo con i valori numerici si otterrà:
· b= 9,216 cm
NB: ho tenuto 3 cifre significative dopo la virgola per rendere il risultato finale più attendibile possibile
Scopri di più sui teoremi di seno e coseno
Successivamente si andrà a trovare l’ultima incognita c applicando la stessa logica
· 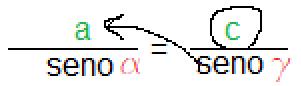
Isolo l’incognita con la stessa procedura applicata precedentemente
· 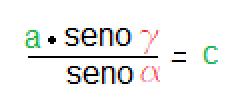
Sostituendo con i valori numerici si otterrà:
C= 8,152 cm
Dopo aver ottenuto l’ultima incognita si andrà a verifica i tre rapporti delle lunghezze e il seno dei loro rispettivi angoli opposti:
· 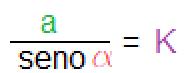
· K= 10,64
· 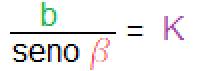
· K= 10,64
· 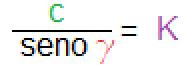
· K=10,64
Conclusione: La costante K come da risultato si ripete in tutti e tre i rapporti, a dimostrazione che la definizione è corretta.
Teorema del coseno
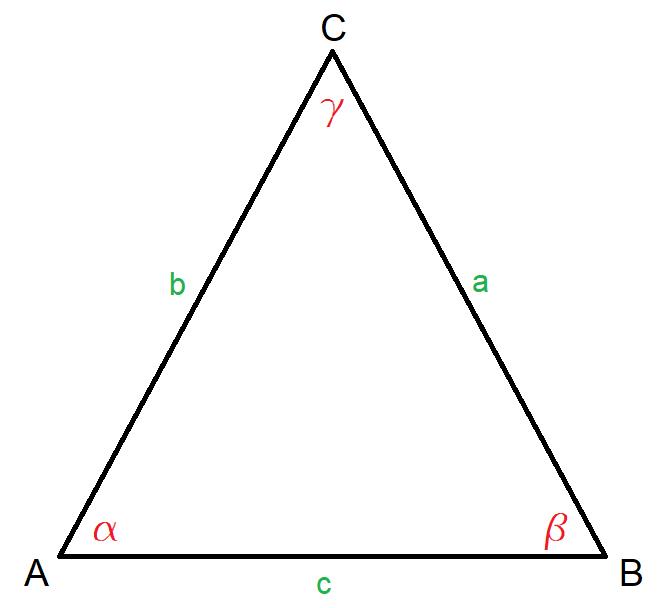
Consideriamo un triangolo qualsiasi dove abbiamo:
· a, b e c che rappresentano la lunghezza dei lati
· a, b e g che rappresentano gli angoli opposti alle lunghezze a, b e c
definizione: in un triangolo qualsiasi, il quadrato della lunghezza di uno dei tre lati è uguale alla somma dei quadrati delle lunghezze degli altri due lati, diminuito del doppio del prodotto tra le lunghezze dei due lato e del coseno dell’angolo compreso dei medesimi.
Esaminando meglio tale definizione si può scrivere che:

per quanto riguarda il triangolo rettangolo quando si andrà a determinare l’ipotenusa, il coseno dell’angolo retto (90°) darà come risultato 0 e di conseguenza la formula si riduce a :
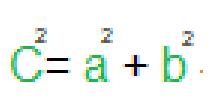
Esempio:
se vogliamo determinare la lunghezza c ci basterà svolgere il teorema tenendo conto che c è al quadrato e di conseguenza al risultato finale basterà metterlo sotto la radice quadrata

Prendendo sempre i valori precedenti applicati nel teorema dei seni, proviamo a svolgere il problema:
C= 8,152 (come valore è uscito lo stesso come lo è stato per il teorema dei seni)
Proviamo invece a calcolare invece angolo g che sarà dato alla formula inversa, successivamente dopo aver trovato il coseno di g basterà semplicemente fare un arc coseno per trovare il valore effettivo. Ma vediamo la formula nel complesso.
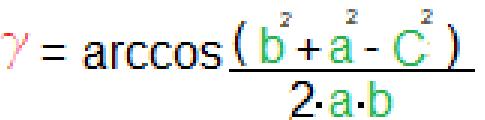
Sviluppando con i numeri si ottiene g= 50° ossia lo stesso valore con il teorema dei seni

