Soluzione primo quesito prova di matematica (maturità 2024)
Riportiamo qui di seguito l'esercizio della seconda prova di maturità dell'anno scolastico 2023/2024. La seconda prova di matematica è rivolta a tutti gli studenti dei licei scientifici.
Ricordiamo che la prova di matematica è strutturata in 2 parti differenti: la prima riguarda quesiti (8 ) di cui ne vengono scelti alcuni dagli studenti. La seconda parte riguarda 2 problemi da risolvere, di cui uno in genere comprende lo studio di una funzione.
La prova di matematica del 2024 prevedeva lo svolgimento di 4 quesiti a scelta su 8, tutti su argomenti del programma di liceo scientifico degli ultimi anni del percorso.
Il primo quesito proposto riguardava lo studio di un triangolo rettangolo. Proviamo a risolverlo assieme.
E' dato un triangolo ABC, rettangolo in B. Dimostrare che tale triangolo è isoscele se e solo se l'altezza BH relativa all'ipotenusa è congruente a metà ipotenusa.
Per prima cosa, proviamo a disegnare il triangolo rettangolo, così come ci viene detto dal testo del quesito: evidenziamo l'altezza BH relativa all'ipotenusa. Si può facilmente notare che il triangolo è composto dai due cateti AB e BC e dall'ipotenusa AC.
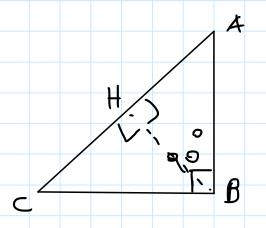
Il triangolo è rettangolo in B.
Notiamo anche che l'altezza relativa all'ipotenusa divide il triangolo ABC in altri due triangoli rettangoli, in quanto l'altezza cade perpendicolarmente sul lato AC per definizione ( si formano dunque due triangoli da 90° ciascuno) .
Iniziamo applicando subito il teorema di Pitagora, valido per i triangoli rettangoli. Per tale teorema abbiamo: BH2 =BC2 -CH 2= AB 2-AH 2
Questo perché, come abbiamo accennato anche sopra, si formano due triangoli rettangoli BHC e BHA, di cui è in comune il cateto BH.
Tra le ipotesi abbiamo che CH e AH sono uguali (entrambi pari a 1/2 dell'ipotenusa del triangolo intero, ovvero entrambi pari a 1/2 AC ).
Dunque anche i loro quadrati sono uguali, e possono essere semplificati dall'uguaglianza: BH 2=BC 2-CH 2=AB 2-AH2
Basta quindi sostituire al posto di AH 2 il valore CH 2 . Troviamo allora che BC 2=AB 2 . Ovvero: BC 2-AB 2=0
Cioè, utilizzando il prodotto notevole differenza di quadrati: (BC-AB)(BC+AB)=0.
Adesso sappiamo anche che BC+ AB non può essere uguale a zero (sono due lunghezze, entrambi positive: la somma di due numeri positivi non sarà mai uguale a zero!)
Allora BC-AB=0 e di conseguenza BC=AB ,come volevamo dimostrare.
Notiamo, infine, che se CH fosse diverso da AH, anche i quadrati sarebbero diversi. Affinchè BC=AB dobbiamo avere BC 2-AB 2=0, come visto sopra.
BC 2-CH 2=AB 2-AH 2 -->BC 2-AB 2= CH 2-AH 2=0 se e solo se CH 2-AH 2=0
Applicando nuovamente il prodotto notevole differenza di quadrati, otteniamo: (CH- AH) (CH+AH)=0 quindi CH-AH=0, cioè CH deve essere uguale ad AH.
Concludiamo che l'unico modo per avere i cateti BC ed AB uguali, è che siano anche CH ed AH uguali.
Hai bisogno di ripetizioni di matematica?


