Le funzioni goniometriche: seno, coseno, tangente e cotangente

Le funzioni goniometriche sono delle funzioni matematiche che mettono in relazione gli angoli di un triangolo con i suoi medesimi lati.

Lezioni di matematica online

Si possono distinguerne diversi tipi tra cui: seno (sin), coseno (cos), la tangente (tan) e la cotangente (cot). Essi possono essere rappresentati tramite una circonferenza, detta circonferenza goniometrica, che è uno strumento utile nello studio della trigonometria, permettendo così di analizzare i valori che assumono le funzioni e di calcolarle in qualunque angolo. Essa viene rappresentata graficamente nel seguente modo:

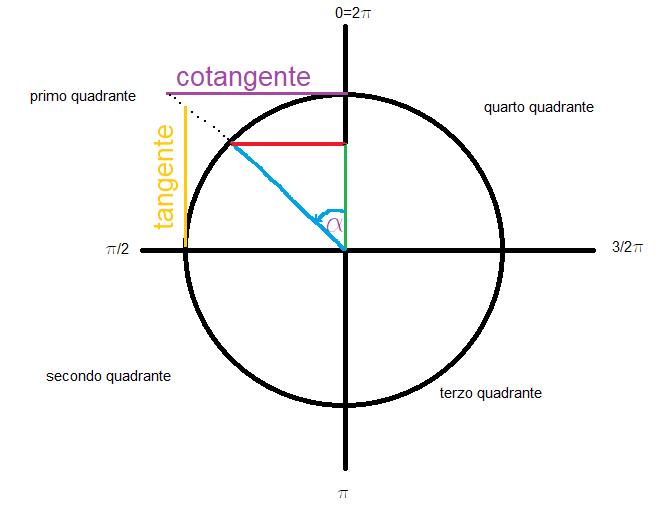
Dove troviamo 4 quadranti di 90° ciascuno, atto a formare un giro di 360°

- Seno (sin): è definito come il rapporto tra il cateto opposto all’angolo e la lunghezza dell’ipotenusa, ma tuttavia, nel contesto della circonferenza unitaria, il seno di un angolo viene rappresentato come l’ordinata del punto sulla circonferenza unitaria che corrisponde all’angolo.

Il seno di un angolo presenta delle caratteristiche osservabili e facilmente individuabili, tra cui;

·         Periodicità: il seno è una funzione periodica con un periodo di 2p radianti oppure di 360°. Il che significa che si ripete ogni 360°, facilmente rappresentabile dal grafico del seno.

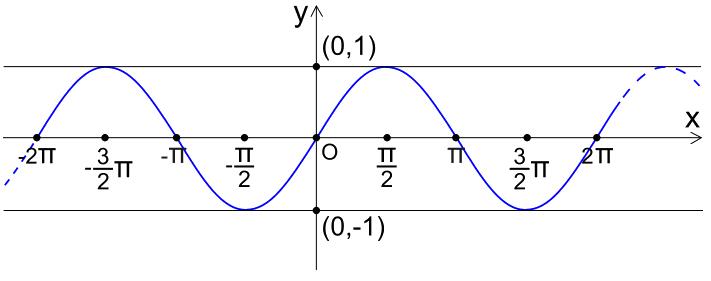
·         Intervallo di valori: il seno di un angolo può assumere valori compresi tra -1 e +1 dato che la circonferenza presenta un raggio di 1

·         Simmetria dispari: il seno è una funzione dispari. Questo intende che il grafico del seno è simmetrico rispetto all’origine.

Scopri di più sulle funzioni goniometriche

Rappresentazione grafica tramite la circonferenza goniometrica:

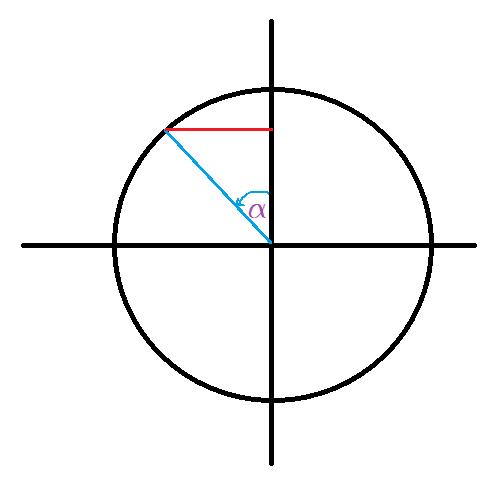
Di conseguenza il seno dell’angolo a è il seguente:

·        

-coseno (cos): è definito come il rapporto tra il cateto adiacente all’angolo e la sua ipotenusa, questa definizione può essere estesa a tutti gli angoli nel piano, utilizzando il concetto di circonferenza unitaria. Ma tuttavia nel contesto della circonferenza unitaria, il coseno di un angolo è definito come l’ascissa del punto sulla circonferenza unitaria che corrisponde all’angolo.

Il coseno di un angolo presenta delle caratteristiche osservabili e facilmente individuabili, tra cui;

·         Periodicità: il coseno è una funzione periodica con un periodo di 2p radianti oppure di 360°. Il che significa che si ripete ogni 360° facilmente rappresentabile dal grafico del coseno.

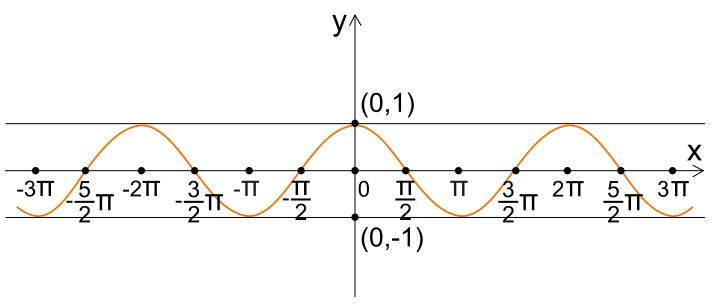
·         Intervalli di valori: il coseno di un angolo può assumere valori compresi tra -1 e +1, dato che la circonferenza presenta un raggio di 1.

·         Simmetria pari: il coseno è una funzione pari, il che indica che il grafico del coseno è simmetrico rispetto all’asse delle ordinate.

Rappresentazione grafica tramite la circonferenza goniometrica:

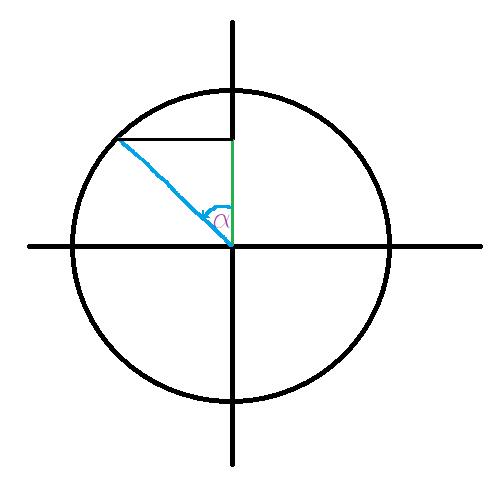
Di conseguenza il coseno dell’angolo a è il seguente:

·        

-tangente (tan): è definita come il rapporto tra il seno e il coseno dell’angolo.

La tangente di un angolo presenta delle caratteristiche osservabili e facilmente individuabili, tra cui;

·         Non divisibile per zero: la tangente non è definita quando il coseno presenta come valore zero

·         Periodicità: la tangente presenta una periodicità di p radianti o 180°. Il che significa che si ripete ogni 180° facilmente rappresentabile dal grafico della tangente.

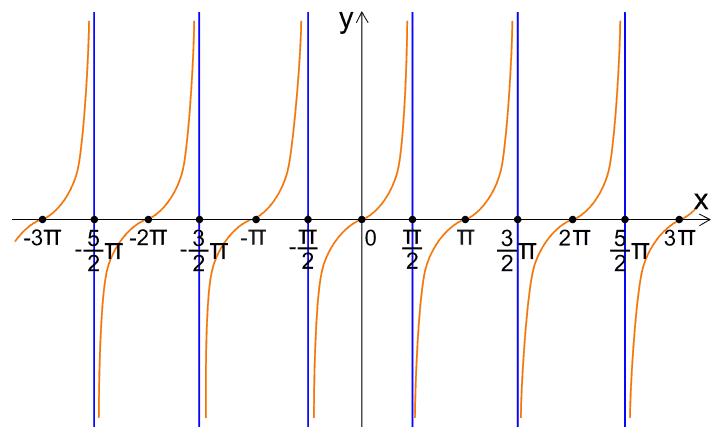
·         Intervallo dei valori: la tangente assume dei valori tra meno infinito e più infinito

·         Simmetria dispari: presenta una funzione dispari come da grafico

Rappresentazione grafica tramite la circonferenza goniometrica:

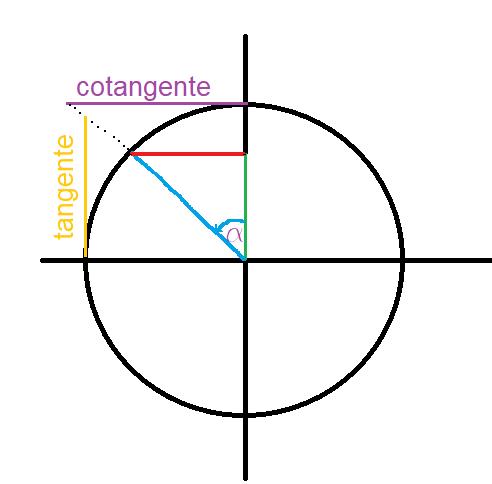
Di conseguenza la tangente dell’angolo a è la seguente:

·        

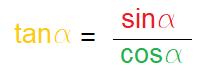
-la cotangente (cot): è una delle funzioni goniometriche principali ed è la reciproca della tangente di un angolo. Viene definita come il rapporto tra il coseno e il seno dell’angolo.

Per determinare graficamente la cotangente, sarà necessario tracciare la funzione cot a in funzione di a. è considerata una funzione periodica che ha asintoti verticali nei punti in cui il seno si annulla. Questi asintoti corrispondono agli angoli nel triangolo per i quali il lato opposto è uguale a 0, ovvero gli angoli multipli di p.

Scopri gli insegnanti di matematica vicino a te!

Domenico 1ª lezione gratis (10)10100

Luca 1ª lezione gratis (24)10100

la cotangente di un angolo presenta delle caratteristiche osservabili e facilmente individuabili, tra cui;

·         Non divisibile per zero: la cotangente non è definita quando il seno dell’angolo è pari a zero

·         Periodicità: presenta una periodicità di 180° facilmente rappresentabile dal grafico della cotangente

·         Intervallo di valori: la cotangente può assumere valori reali compresi tra meno infinito e più infinito

·         Simmetria dispari: la cotangente è una funzione dispari

Rappresentazione grafica tramite la circonferenza goniometrica:

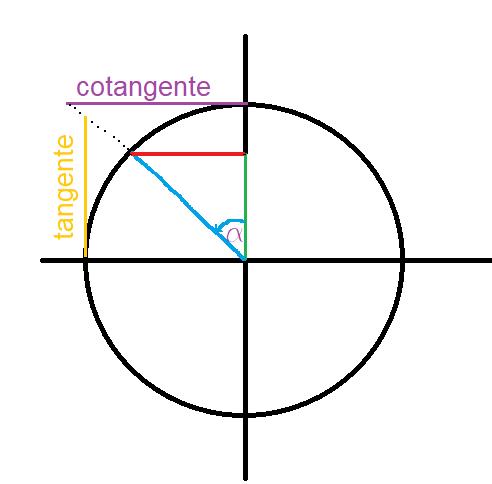
Di conseguenza la cotangente dell’angolo a è la seguente:

·        

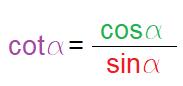
La cotangente viene utilizzata in vari ambiti matematici, fisici e ingegneristici, ed è una funzione goniometrica importante che fornisce delle informazioni sul rapporto tra i lati di un triangolo rettangolo, oltre ad essere impiegata per risolvere una vasta gamma di problemi teorici e pratici.