Determinazione dell'errore nelle misure dirette
Qualsiasi misurazione si effettua è intrinsecamente imprecisa e tralasciando tutti gli errori sistematici (che avvengono costantemente) per difetto dello strumento di misura o alterazione psicofisica dell’osservatore ci occupiamo solo di quelli dovuti alla sensibilità dello strumento e degli errori accidentali.
- Si definisce sensibilità dello strumento s il minimo valore rilevato dallo strumento di misura. Ad esempio un righello millimetrato ha come sensibilità proprio 1mm, in quanto non riesce a misurare quantità più piccole. Se si prende un metro con 100 tacche la sensibilità è al centimetro, per la stessa ragione. Supponendo di misurare con entrambi la quantità di 35 cm nel primo caso posso aver sbagliato di 1 mm e dunque la mia misura varierà tra 34,9 cm 3 35,1 cm. Si scrive quindi la misura considerando tutte le cifre certe e la cifra incerta a cui si somma/sottrae l’incertezza (ovvere l’errore assoluto, che nelle misure singole coincide con la sensibilità dello strumento) per racchiudere il range di valori entro cui può variare la misura. Nel caso del metro a cento tacche la misura varierà tra 34 e 36 centimetri e anche in quel caso bisogna considerare l’incertezza data dalla misurazione. Nella seguente tabella si mostra la scrittura delle misure nei due casi

-
Indipendentemente dalla sensibilità dello strumento, per una migliore stima della misura può essere utile ricorrere a misure ripetute per essere sempre più certi del valore. Dette V1, V2,..., Vn le n misurazioni, Vm il valor medio, Vmax e Vmin rispettivamente il valore massimo e il valore minimo misurato nelle N misurazioni si ha:
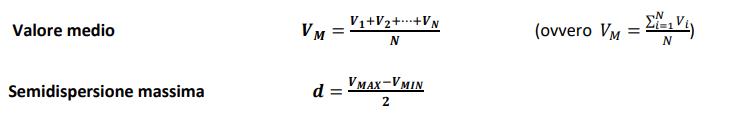
La semidispersione massima pur essendo una stima grossolana della variabilità della misura è sufficiente per misure che non richiedono un’estrema precisione.
- Si definisce errore assoluto il più grande tra i valori della sensibilità dello strumento e della semidispersione massima:
![]()
Una misura va scritta come il suo valor medio con range di intervallo dato dall’errore assoluto, si ricorda che l’errore assoluto va scritto con una sola cifra significativa e che quindi la misura avrà come cifra incerta quella dell’errore assoluto.
![]()
- Si definisce inoltre l’errore relativo come il rapporto tra l’errore assoluto e il valor medio; tale misura è un valore di quanto precisa è la misura infatti minore è l’errore relativo più precisa è la misura. Per tale ragione si usa spesso l’errore relativo percentuale che semplicemente mette in forma di percentuale l’errore relativo, moltiplicandolo per 100. Anche l’errore relativo andrebbe scritto con una sola cifra significativa, ma nell’uso comune spesso si usano più cifre significative.

Esempio: si misura il lato di un tavolo sette volte con un metro millimetrato ottenendo le misure:22,4 cm, 22,6 cm, 22,7cm, 22,1cm , 22,3cm , 22,1cm , 22,3 cm. Raccogliere in una tabella le misure e, dopo aver determinato l'errore assoluto, scrivere la misura con la relativa incertezza, e trovare l'errore relativo e l'errore relativo percentuale.



