I numeri: una classificazione degli insiemi numerici e il loro utilizzo nella realtà

Lezione di matematica online: gli insiemi numerici

Un numero è un concetto matematico astratto utilizzato per esprimere quantità, per ordinare elementi in una successione, o per identificare un elemento univoco. Può indicare "quanti sono" gli elementi di un insieme (numero cardinale), "quale" è la posizione di un elemento (numero ordinale), o servire come etichetta o simbolo.

Le funzioni dei numeri

Contare

Per esprimere una quantità, ad esempio, "ho comprato tre mele".

Indicare la posizione

Per stabilire l'ordine, ad esempio, "è arrivato al primo posto".

Misurare

Per quantificare grandezze fisiche, come lunghezze o pesi.

Identificare

Per dare un nome univoco a un elemento, come un numero di telefono o il numero di una casa.

Calcolare

Per eseguire operazioni matematiche, come sommare o moltiplicare, che ci permettono di risolvere problemi complessi.

➡️ Scopri le migliori app per studiare matematica online in questo post!

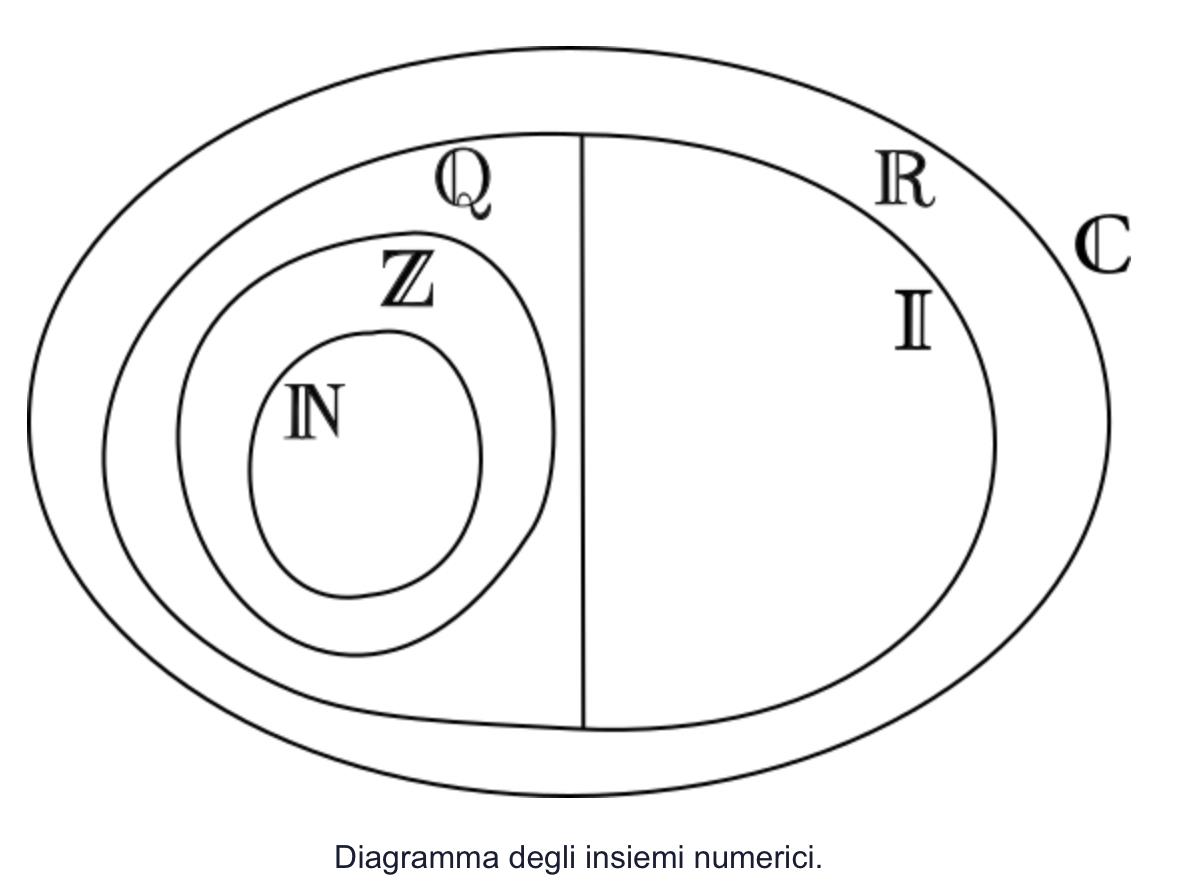
Classificazione dei numeri

I numeri sono classificati in:

• Naturali (N)

• Interi (Z)

• Razionali (Q)

• Irrazionali (I)

• Reali (R)

I numeri naturali (N)

I numeri naturali (N) sono: 1, 2, 3, 15, 88, 104, ecc.
Essi sono definiti come numeri interi non negativi che partono dallo zero e proseguono a destra verso l'infinito positivo.

I numeri interi (Z)

I numeri interi (Z) sono: -43, -27, -6, +5, +13, +33, ecc.
Essi sono definiti come numeri finiti preceduti o dal segno meno (-) o dal segno più (+).

I numeri razionali (Q)

I numeri razionali (Q) sono: -3/2, 5/3, -17/8, ecc.
Essi sono definiti come numeri espressi da una frazione, preceduti da un segno positivo o negativo.

I numeri irrazionali (I)

I numeri irrazionali (I) sono: π (pi greco), √5, √13, ecc.
Essi sono numeri che non possono essere espressi da una frazione. Sono tutti numeri decimali illimitati non periodici.

I numeri reali (R)

I numeri reali (R) rappresentano l'unione di tutti gli insiemi precedentemente descritti.

Uno dei limiti dei numeri reali è l'impossibilità di estrarre i numeri negativi da radici con indici pari.
Per tale ragione sono stati introdotti anche i numeri complessi (C).

Esempi sull'utilizzo dei numeri nella realtà

• Numeri naturali: per contare le quantità

• Numeri interi: per indicare la temperatura

• Numeri razionali: per indicare la porzione di una torta rispetto all'intero

• Numeri irrazionali: per indicare valori indefiniti (come il pi greco)

L'utilizzo di questi numeri ci permette di svolgere tutte le operazioni matematiche necessarie sia ad analisi di natura scolastica ed accademica, sia allo svolgimento di pratiche di uso quotidiano come la spesa, il calcolo di misure di lavori di costruzione, il dosaggio di ingredienti per la realizzazione di una ricetta, ecc.

Le operazioni matematiche fondamentali

Addizione

Operazione che a partire da due o più numeri indicanti quantità omogenee (detti addendi o termini) dà come risultato (totale o somma) il numero costituito dalle unità del primo, del secondo, ecc.

Sottrazione

L'operazione che associa a due numeri un terzo numero, detto differenza, che sommato al minore dei due dà il maggiore; è pertanto, fra le quattro operazioni fondamentali, l'inverso dell'addizione.

Moltiplicazione

L'operazione che consente di associare a due numeri, chiamati fattori, un terzo numero, chiamato prodotto, al quale si perviene addizionando tanti addendi uguali al primo numero quante sono le unità del secondo e così via.

Divisione

L'operazione ha per scopo di determinare quante volte un numero (il divisore) è contenuto in un altro (il dividendo).

Operazioni più complesse

Tutte le altre operazioni più complesse che prevedono il ricorso congiunto alle precedenti (espressioni, equazioni di diverso grado, derivate, integrali, studio di funzioni, ecc.)

Hai bisogno di aiuto per comprendere un argomento di matematica?

Contatta un insegnante privato!

Federico 1ª lezione gratis (69)9100

Enrico 1ª lezione gratis (3)10100