Perché “imparare a memoria” la matematica rende poco (e come evitarlo)

La matematica non è solo un insieme di formule da ripetere, ma un linguaggio che permette di interpretare il mondo, risolvere problemi e ragionare in modo logico.
Studiare solo a memoria significa rinunciare alla parte più preziosa della disciplina: la comprensione profonda dei meccanismi che stanno dietro a ogni formula o regola.

Perché è importante capire la matematica e non solo ricordare

Chi studia la matematica come un elenco di regole tende a dimenticare tutto appena cambia il tipo di esercizio.
Capire, invece, permette di riconoscere le connessioni tra gli argomenti, di adattarsi ai problemi nuovi e di sviluppare autonomia di ragionamento, sviluppando una logica che ritornerà sempre utile.
La memoria serve, ma arriva dopo la comprensione — non al suo posto.

Differenza tra memoria utile e memoria passiva

• Memoria utile: deriva dalla pratica e dalla logica. Ricordi una formula perché l’hai capita e applicata molte volte.

• Memoria passiva: è quella che ti fa ripetere meccanicamente i passaggi senza capirne il senso. È fragile e svanisce in fretta.
  Un buon metodo di studio deve puntare alla prima, evitando la seconda.

Come strutturare lo studio della matematica passo per passo

Fase iniziale: capire il problema, non la formula

Ogni argomento matematico parte da un’idea. Prima di imparare la regola, bisogna capire che problema risolve o in alternativa cosa rappresenta nel graficp.
Ad esempio, prima di imparare la formula dell’area del triangolo, chiediti perché serve e da dove viene. Questo attiva la curiosità e rende la formula naturale, non imposta.

Fase centrale: costruire il ragionamento attraverso esempi

Un esercizio ben scelto vale più di dieci formule.
Parti da casi semplici, analizza i passaggi, verbalizza ogni scelta (“perché faccio questo passaggio?”). In questo modo lo studente diventa parte attiva e il cervello collega i concetti anziché memorizzarli in modo isolato.

Fase finale: verifica della comprensione e autovalutazione

Alla fine di ogni argomento, lo studente dovrebbe essere in grado di:

• spiegare il concetto con parole proprie;

• risolvere un esercizio simile senza aiuto;

• individuare dove e perché ha sbagliato.
  Questa riflessione trasforma la conoscenza in competenza reale.

Cosa NON fare: imparare regole a caso, saltare i passaggi, ignorare gli errori

Memorizzare formule senza contesto, cercare scorciatoie o evitare di capire dove si sbaglia è controproducente.
In matematica, sbagliare è parte del processo di apprendimento: ogni errore svela un ragionamento da correggere.

Strumenti e materiali per studiare in modo efficace

Schede ragionate, esercizi progressivi e mappe concettuali

Le schede sintetiche e le mappe aiutano a visualizzare i legami tra argomenti.
Crea un percorso graduale: prima gli esempi guidati, poi esercizi autonomi.
Una mappa di “collegamenti logici” (es. frazioni → proporzioni → percentuali) rende tutto più chiaro e coerente.

Piattaforme e risorse utili per lo studio online

• GeoGebra per visualizzare funzioni e figure geometriche.

• Desmos per comprendere graficamente le equazioni.

• Khan Academy o YouTube EDU per rivedere concetti con spiegazioni alternative.
  L’obiettivo non è sostituire il tutor, ma rinforzare la comprensione con più prospettive.

Come prendere appunti efficaci durante lo studio

Scrivere a mano aiuta la memoria concettuale.
Meglio pochi appunti ma ragionati: formule spiegate con parole proprie, esempi chiave e domande aperte (“perché questo passaggio funziona?”).
L’atto di spiegarsi le cose è già un modo per consolidarle.

Come trasformare la conoscenza in vera padronanza della matematica

Strategie per passare dalla teoria alla pratica

Dopo aver compreso la teoria, bisogna metterla alla prova.
Alterna studio e applicazione, risolvi problemi nuovi, cambia i numeri o le condizioni per vedere se il ragionamento regge.
Capire quando applicare una formula vale più del ricordarla.

Rendere lo studio costante e gratificante

La matematica è come una lingua: va praticata.
Crea una routine breve ma quotidiana, alternando ripasso, esercizi e momenti di verifica.
Ogni piccolo miglioramento deve essere riconosciuto: la fiducia nasce dai progressi, non dai voti.

Esempio pratico: soluzioni di un'equazione di secondo grado, parabola

Nella mia esperienza come insegnante di matematica, ho riscontrato spesso quanto la comprensione profonda valga più della semplice memorizzazione.
Un esempio lampante è quello delle equazioni di secondo grado.

Molti studenti imparano a memoria la formula del delta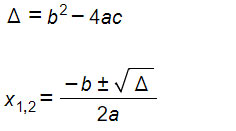 

senza davvero sapere cosa stiano calcolando. Così, basta un piccolo errore nei segni o nei passaggi per non capire più nulla. Senza contare che per alcuni studenti potrebbe essere difficile da ricordare a memoria.

Ma se si osserva l’equazione graficamente, tutto diventa più intuitivo: l’equazione di secondo grado rappresenta una parabola, e le soluzioni x1, x2 non sono altro che i punti in cui la parabola interseca l’asse x.
Capire questo concetto visivamente aiuta a dare senso alla formula:

• Se il delta è positivo, la parabola taglia l’asse in due punti distinti.

• Se il delta è zero, la parabola tocca l’asse in un solo punto (radice doppia).

• Se il delta è negativo, la parabola non lo tocca affatto (nessuna soluzione reale).

Con un semplice grafico, lo studente “vede” quello che la formula descrive in modo astratto.
E così, anche la formula del delta smette di essere una sequenza da ricordare e diventa uno strumento logico per interpretare ciò che accade sul piano cartesiano.

Domande frequenti degli studenti sulla matematica

• “Ma se non imparo a memoria, come faccio a ricordare?”
  → Capendo il significato, la memoria viene da sé.

• “Perché dimentico tutto dopo poco?”
  → Probabilmente hai studiato senza collegare i concetti.

• “Come faccio a migliorare se non mi piace la matematica?”
  → Cambiando approccio: meno ripetizione, più curiosità e logica applicata.