Lezioni di matematica: spieghiamo il Teorema di Pitagora

Possiamo cominciare col dire che il Teorema di Pitagora è uno dei teoremi più conosciuti di tutta la storia della matematica. Le sue origini sono molto incerte  e molto antiche nel senso che la sua applicazione era già conosciuta prima dello stesso Pitagora. Già i Babilonesi lo applicavano nei loro problemi, se ne trova traccia nei popoli asiatici  come India e Cina.  Appare certo comunque, che si deve a questo matematico la sua generalizzazione. È uno dei teoremi più dimostrati e di queste dimostrazioni ne esistono centinaia utilizzando sia argomenti di tipo geometrico che algebrico. 

Insegnanti di matematica nella tua zona

Alessia 1ª lezione gratis (6)10100

Luca 1ª lezione gratis (1)10100

Viene studiato principalmente nella seconda media inferiore e le sue applicazioni sono innumerevoli. Infatti sebbene sia un teorema che riguarda i triangoli rettangoli, molte figure geometriche piane o anche solide, possiamo dire "contengono triangoli rettangoli". Il caso più semplice che mi viene in mente è un rettangolo, basta tracciare una delle due diagonali e la figura viene suddivisa in due triangoli rettangoli congruenti e quindi dove è possibile applicare il teorema.

Anche i poligoni regolari si possono suddividere in triangoli rettangoli. Basta suddividere il poligono in triangoli isosceli e tracciare per ognuno l'altezza che poi  è l'apotema.

Altre applicazioni pratiche sono nel campo dell'ottica ad esempio (lenti di ingrandimento, telescopi, microscopi), nelle costruzioni urbanistiche, in fisica nella scomposizione delle forze... insomma si potrebbe fare un elenco lunghissimo.

Il suo enunciato è semplicissimo, mette in relazione i due cateti con l'ipotenusa:

• "In ogni triangolo rettangolo la somma delle aree dei quadrati costruiti sui cateti è uguale all'area del quadrato costruito sull'ipotenusa."

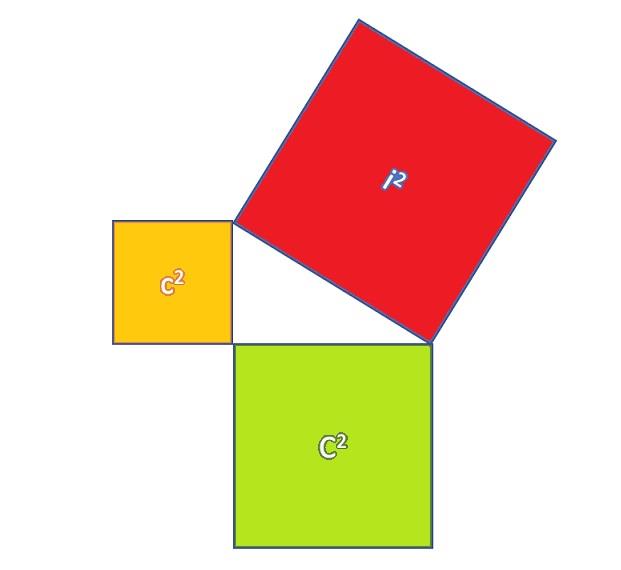
Come si nota dalla figura la somma dell'area verde con l'area gialla da l'area rossa.

In forma algebrica:

C^2 + c^2 = i^2

Non mi soffermerò sulla dimostrazione che come ho detto ce ne sono centinaia e nemmeno su qualche tipo di problema. 

Preferisco dire qualcosa che forse viene detto poco nelle scuole e cioè le sue generalizzazioni. Con questo non intendo la generalizzazione data da Pitagora, ma in un ambiente più vasto.

La prima generalizzazione possiamo chiamarla "il teorema di Pitagora applicato a tutti i tipi di triangoli e non solo a quelli rettangoli". Infatti con qualche piccola modifica possiamo scrivere la seguente relazione che vediamo in figura:

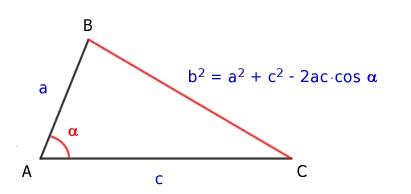
Qui ci vuole qualcosa di più riguardo ad argomenti di seconda media, ma già si può trovarne le applicazioni in fisica (prima superiore o in seconda)  quando si studia la dinamica. Il triangolo in figura non è rettangolo e la formula scritta è detta teorema di Carnot o del coseno. Come si può notare in figura viene calcolata la misura del lato rosso ed è composta da una prima parte dove compaiono i lati elevati alla seconda che rispecchia esattamente Pitagora e da una sottrazione di qualcos'altro; il teorema di Pitagora si ha quando l'angolo alfa misura 90° dove il coseno vale 0. Diciamo che il teorema di Pitagora è un caso particolare del teorema di Carnot (1753-1823).

Articolo correlato Lezioni di matematica: come si fanno le frazioni

Se trovi difficile eseguire esercizi di matematica sulle frazioni, dovresti leggere questo articolo, dove abbiamo condensato alcuni suggerimenti per creare delle piccole lezioni di matematica per capi...

Un'altra generalizzazione può essere vista non sul tipo di triangolo, ma attraverso il poligono che si vuole costruire sui cateti e sull'ipotenusa.

Diamo prima la definizione di similitudine: la similitudine è una trasformazione geometrica che lascia inalterati gli angoli della figura, ma ne cambia il valore dei lati, del perimetro e dell'area.

Questa definizione sembra non avere niente a che fare con il teorema di Pitagora, ma in realtà è il punto principale. Comunque senza approfondire troppo, si può dire che:

• "se i poligoni (irregolari o regolari) costruiti sui cateti e sull'ipotenusa sono simili tra loro, allora la somma delle aree dei poligoni costruiti su cateti è equivalente all'era del poligono costruito sull'ipotenusa". 

Il teorema di Pitagora risponde esattamente a questa definizione ed è il caso più semplice: infatti i quadrati sono figure tutte simili tra di loro per definizione. 

Questa generalizzazione è un po' meno intuitiva, ma si può dimostrare facilmente per via algebrica. Voglio lasciare un quesito finale; ho dato due generalizzazioni del teorema di Pitagora, una che vale per ogni triangolo, ma che mantiene la costruzione di quadrati sui lati dello stesso triangolo e una che mantiene fisso il triangolo rettangolo, ma fa variare il poligono costruito sui lati. La domanda è: si possono fondere in un unica generalizzazione?